How to Calculate Torque

Finding Torque for Perpendicular Forces

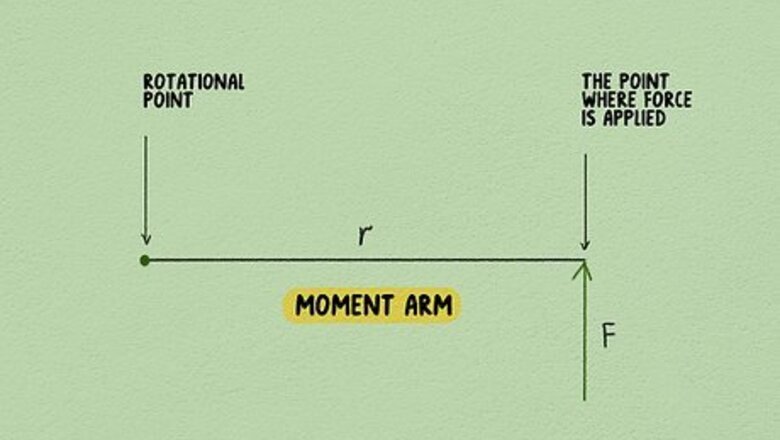
Find the length of the moment arm. The distance from the axis or rotational point to the point where force is applied is called the moment arm. This distance is typically expressed in meters (m). Since torque is a rotational force, this distance is also a radius. For this reason, you'll sometimes see it represented with an "r" in the basic torque equation.

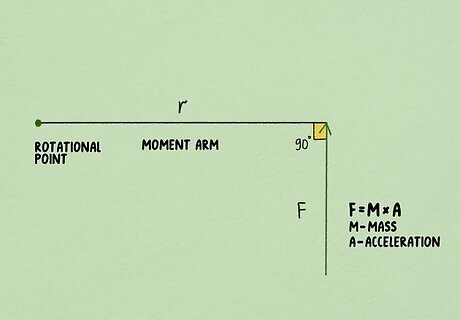
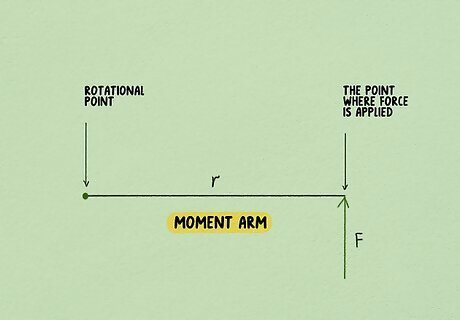
Work out the force being applied perpendicular to the moment arm. The force applied perpendicular to the moment arm produces the greatest torque. The simplest torque equation assumes the force is being applied perpendicular to the moment arm. In torque problems, you'll typically be given the magnitude force. However, if you have to work it out yourself, you'll need to know the mass of the object and the acceleration of the object in m/s. According to Newton's Second Law, force is equal to mass times acceleration ( F = m × a {\displaystyle F=m\times a} {\displaystyle F=m\times a}).

Multiply the force times the distance to find the torque. The basic formula for torque is τ = F × r {\displaystyle \tau =F\times r} {\displaystyle \tau =F\times r}, where torque is represented by the Greek letter tau (τ) and equals the force (F) times the distance (or radius, r). If you know the magnitude of the force (in Newtons) and the distance (in meters), you can solve for the torque, expressed in newton-meters (N∙m). For example, suppose you have a force perpendicular to your object exerting 20 Newtons of force on the object 10 meters from the axis. The magnitude of the torque is 200 N∙m: τ = 20 × 10 = 200 {\displaystyle \tau =20\times 10=200} {\displaystyle \tau =20\times 10=200}

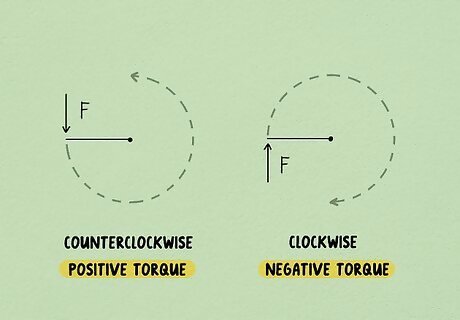
Show the direction of the force with positive or negative torque. You now know the magnitude of the torque, but you don't know if it's positive or negative. This depends on the direction of the rotation. If the object is rotating counterclockwise, the torque is positive. If the object is rotating clockwise, the torque is negative. For example, if the object is moving clockwise and the magnitude of the torque is 200 N∙m, you would express this as -200 N∙m of torque. No sign is necessary if the magnitude of the torque is positive. The value given for the magnitude of the torque remains the same. If a negative sign appears before the value, it simply means that the object in question is rotating clockwise.

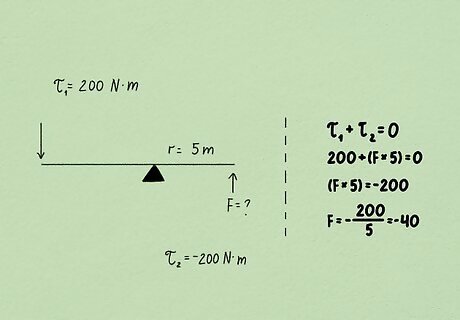
Total individual torques around a given axis to find the net torque (Στ). It's possible to have more than one force acting on an object at a different distance from the axis. If one force is pushing or pulling in the opposite direction of the other force, the object will rotate in the direction of the stronger torque. If the net torque is zero, you have a balanced system. If you're given the net torque but not some other variable, such as the force, use basic algebraic principles to solve for the missing variable. For example, suppose you're told that the net torque is zero. The magnitude of the torque on one side of the axis is 200 N∙m. On the other side of the axis, force is being exerted from the axis in the opposite direction 5 meters from the axis. Since you know that net torque is 0, you know that the 2 forces must add up to 0, so you can construct your equation to find the missing force: 200 + ( F × 5 ) = 0 {\displaystyle 200+(F\times 5)=0} {\displaystyle 200+(F\times 5)=0} F × 5 = − 200 {\displaystyle F\times 5=-200} {\displaystyle F\times 5=-200} F = − 200 5 {\displaystyle F=-{\frac {200}{5}}} {\displaystyle F=-{\frac {200}{5}}} F = − 40 {\displaystyle F=-40} {\displaystyle F=-40}

Figuring out the Torque for Angled Forces

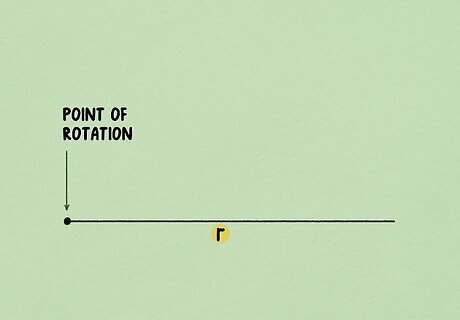
Start with the distance of the radial vector. The radial vector is the line that extends from the axis or point of rotation. It could also be any object, such as a door or the minute-hand of a clock. The distance to measure for the purposes of calculating torque is the distance from the axis to the point where the force is applied to rotate the vector. For most physics problems, this distance is measured in meters. In the torque equation, this distance is represented by "r" for radius or radial vector.

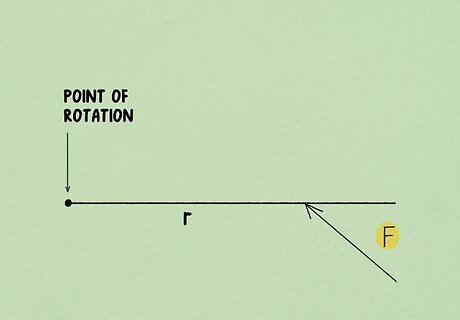
Work out the amount of force being applied. In most torque problems, this value will also be given to you. The amount of force is measured in Newtons and will be applied in a particular direction. However, rather than being perpendicular to the radial vector, the force is applied at an angle, giving you a radial vector. If you're not provided with the amount of force, you would multiply mass times acceleration to find the force, which means you would need to be given those values. You might also be given the torque and told to solve for the force. In the torque equation, force is represented by "F."

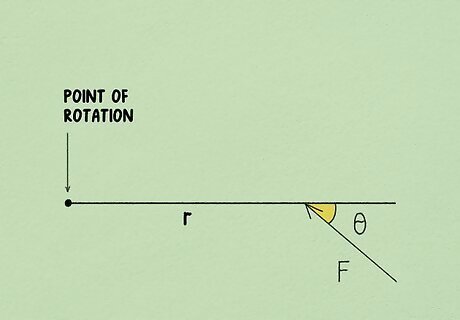
Measure the angle made by the force vector and the radial vector. The angle you measure is the one to the right of the force vector. If the measurement isn't provided for you, use a compass to measure the angle. If the force is being applied to the end of the radial vector, extend the radial vector out in a straight line to get your angle. In the torque equation, this angle is represented by the Greek letter theta, "θ." You'll typically see it referred to as "angle θ" or "angle theta."

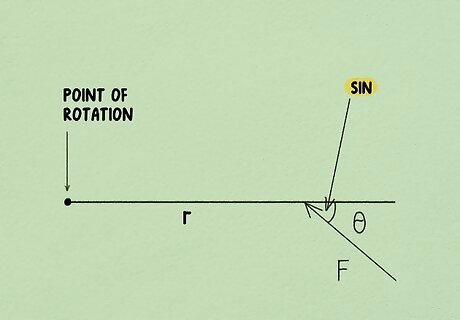
Use your calculator to find the sine of the angle θ. In the torque equation, you multiply the distance of the radial vector and the amount of force with the sine of the angle you just measured. Put the angle measurement into your calculator, then press the "sin" button to get the sine of the angle. If you were determining the sine of the angle by hand, you would need the measurements for the opposite side and the hypotenuse side of a right triangle. Since most torque problems don't involve making exact measurements, however, you shouldn't have to worry about this.

Multiply the distance, force, and sine to find the torque. The full formula for torque when you have angled force is τ = r × F × s i n θ {\displaystyle \tau =r\times F\times sin\theta } {\displaystyle \tau =r\times F\times sin\theta }. The result is expressed in newton-meters (N∙m). For example, suppose you have a radial vector 10 meters long. You're told that 20 Newtons of force is being applied to that radial vector at a 70° angle. You would find that the torque is 188 N∙m: τ = 10 × 20 × s i n 70 ∘ = 10 × 20 × 0.94 = 188 {\displaystyle \tau =10\times 20\times sin70^{\circ }=10\times 20\times 0.94=188} {\displaystyle \tau =10\times 20\times sin70^{\circ }=10\times 20\times 0.94=188}

Determining Torque with Moment of Inertia and Angular Acceleration

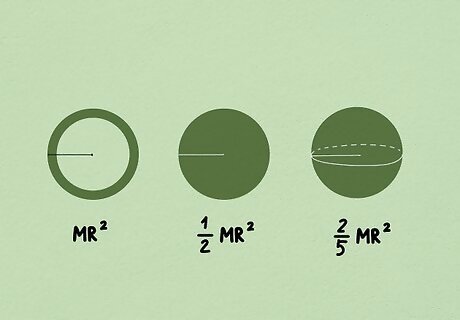
Find the moment of inertia. The amount of torque required to move an object with angular acceleration depends on the distribution of the object's mass, or its moment of inertia, expressed in kg∙m. When the moment of inertia isn't provided, you can also look it up online for common objects. For example, suppose you're trying to figure out the magnitude of torque on a solid disc. The moment of inertia for a solid disc is 1 2 M R 2 {\displaystyle {\frac {1}{2}}MR^{2}} {\displaystyle {\frac {1}{2}}MR^{2}}. The "M" in this equation stands for the mass of the disc, while the "R" stands for the radius. If you know that the mass of the disc is 5 kg and the radius 2 meters, you can determine that the moment of inertia is 10 kg∙m: 1 2 ( 5 × 2 2 ) = 1 2 ( 5 × 4 ) = 1 2 ( 20 ) = 10 {\displaystyle {\frac {1}{2}}(5\times 2^{2})={\frac {1}{2}}(5\times 4)={\frac {1}{2}}(20)=10} {\displaystyle {\frac {1}{2}}(5\times 2^{2})={\frac {1}{2}}(5\times 4)={\frac {1}{2}}(20)=10}

Determine the angular acceleration. If you're trying to find torque, the angular acceleration will typically be given to you. This is the amount, in radians/s, that the object's velocity is changing as it rotates. Remember that the angular acceleration can be zero if the object is moving at a constant speed and is neither speeding up nor slowing down.

Multiply the moment of inertia by the angular acceleration to find the torque. The full formula for torque using the moment of inertia and the angular acceleration is τ = I α {\displaystyle \tau =\mathrm {I} \alpha } {\displaystyle \tau =\mathrm {I} \alpha }, where "τ" stands for torque, "I" stands for the moment of inertia, and "α" stands for the angular acceleration. If you're trying to find torque, simply multiply the moment of inertia and the angular acceleration to get your result. As with other equations, if you're trying to find one of the other values, you can re-order the equation using common algebraic principles. For example, suppose you know that the moment of inertia for an object is 10 kg∙m. You're also told that the torque is 20 N∙m, but you need to find out the angular acceleration. Since you know that τ = I α {\displaystyle \tau =\mathrm {I} \alpha } {\displaystyle \tau =\mathrm {I} \alpha }, you also know that α = τ I {\displaystyle \alpha ={\frac {\tau }{\mathrm {I} }}} {\displaystyle \alpha ={\frac {\tau }{\mathrm {I} }}}. When you put in the variables you know, you'll find that the angular acceleration for the object is 2 radians/s: α = 20 10 = 2 {\displaystyle \alpha ={\frac {20}{10}}=2} {\displaystyle \alpha ={\frac {20}{10}}=2}