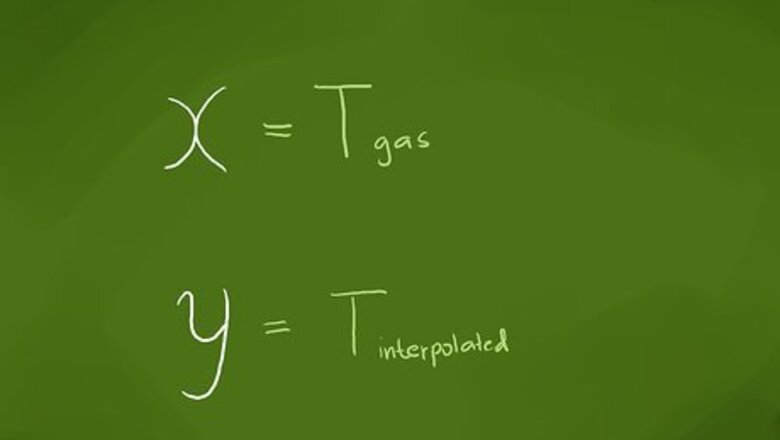
views
X
Research source
is the ability to deduce a value between two values explicitly stated in a table or on a line graph. While many people can interpolate on an intuitive basis, the article below shows the formalized mathematical approach behind the intuition.
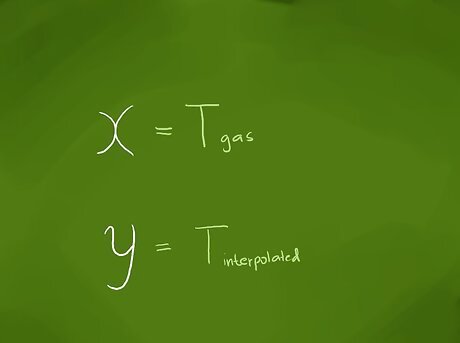
Identify the value for which you want to find a corresponding value. Interpolation can be used for such things as finding a logarithm or trigonometric function value or for the corresponding gas pressure or volume for a given temperature in chemistry. Because scientific calculators have largely replaced logarithmic and trigonometric tables, we’ll use as our example for finding an interpolated value that of finding the pressure of a gas for a temperature whose value isn’t listed in the reference table or as a graph point. For the equation we’ll derive, we’ll represent the value that we want to find a corresponding value for as ‘’x’’ and the interpolated value we want to find as ‘’y’’. (We’ll use these labels, because on a graph, the value we know would be plotted on the horizontal, or x-axis, and the value we’re trying to find would be plotted on the vertical, or y-axis.) Our ‘’x’’ value will be the temperature of the gas, which for this example will be 37 °C (99 °F).
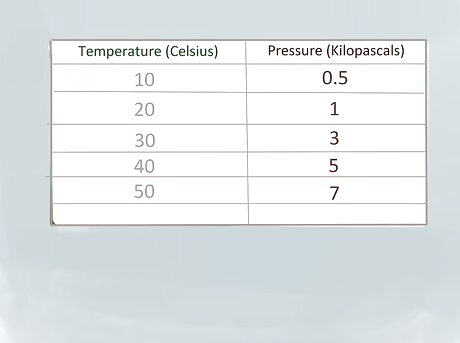
Find the closest values below and above the value of x in the table or on the graph. Our reference table doesn’t give a gas pressure for 37 °C (99 °F), but it does list values for 30 °C (86 °F) and 40 °C (104 °F). The gas pressure at 30 °C (86 °F) is 3 kilopascals (kPa) and the pressure at 40 °C (104 °F) is 5 kPa. Because we’re representing the temperature of 37 °C (99 °F) with ‘’x’’, we’ll represent the temperature of 30 degrees as ‘’x1’’ and the value of 40 degrees as ‘’x2’’.Interpolate Step 2Bullet1 Version 2.jpg Because we’re representing the pressure were trying to find with ‘’y’’, we’ll represent the pressure of 3 kPa at 30 °C (86 °F) as ‘’y1’’ and the pressure of 5 kPa at 40 °C (104 °F) as ‘’y2’’.Interpolate Step 2Bullet2 Version 2.jpg
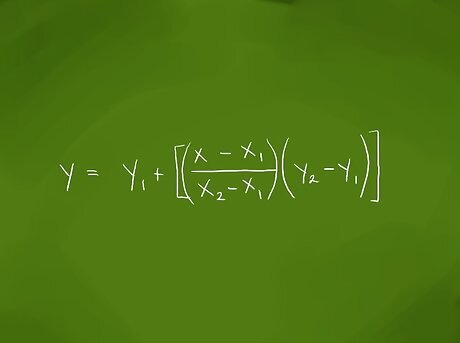
Find the interpolated value mathematically. The equation for finding the interpolated value can be written as y = y1 + ((x – x1)/(x2 - x1) * (y2 - y1)) Plugging in the values for x, x1, and x/2 in their places gives (37 – 30)/(40 -30), which reduces to 7/10 or 0.7.Interpolate Step 3Bullet1 Version 2.jpg Plugging in the values for y1 and y2 at the end of the equation gives (5 – 3) or 2.Interpolate Step 3Bullet2 Version 2.jpg Multiplying 0.7 by 2 gives a product of 1.4. Adding 1.4 to the value of y1, or 3, gives a value of 4.4 kPa. Checking this against our original values, 4.4 falls between 3 kPa at 30 °C (86 °F) and 5 kPa at 40 °C (104 °F), and because 37 is closer to 40 than it is to 30, the result should be closer to 5 kPa than it is to 3 kPa.Interpolate Step 3Bullet3 Version 2.jpg













Comments
0 comment