How to Calculate the Sum of Interior Angles

CityFocus

Editor

posted on 13 years ago — updated on 1 second ago

25
views

A polygon is any closed figure with sides made from straight lines. At each vertex of a polygon, there is both an interior and exterior angle, corresponding to the angles on the inside and outside of the closed figure. Understanding the relationships that govern these angles is useful in various geometrical problems. In particular, it is helpful to know how to calculate the sum of interior angles in a polygon. This can be done using a simple formula, or by dividing the polygon into triangles.

Steps

Using the Formula

Set up the formula for finding the sum of the interior angles. The formula is s u m = ( n − 2 ) × 180 {\displaystyle sum=(n-2)\times 180} sum=(n-2)\times 180, where s u m {\displaystyle sum} sum is the sum of the interior angles of the polygon, and n {\displaystyle n} n equals the number of sides in the polygon. The value 180 comes from how many degrees are in a triangle. The other part of the formula, n − 2 {\displaystyle n-2} n-2 is a way to determine how many triangles the polygon can be divided into. So, essentially the formula is calculating the degrees inside the triangles that make up the polygon. This method will work whether you are working with a regular or irregular polygon. Regular and irregular polygons with the same number of sides will always have the same sum of interior angles, the difference only being that in a regular polygon, all interior angles have the same measurement. In an irregular polygon, some of the angles will be smaller, some of the angles will be larger, but they will still add up to the same number of degrees that are in the regular shape.

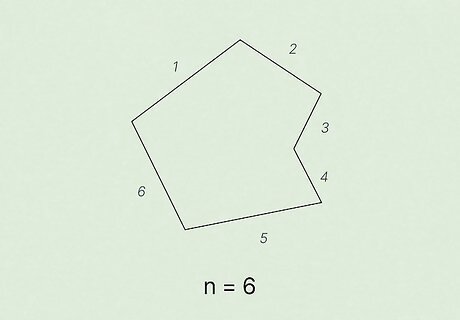
Count the number of sides in your polygon. Remember that a polygon must have at least three straight sides. For example, if you want to know the sum of the interior angles of a hexagon, you would count 6 sides.

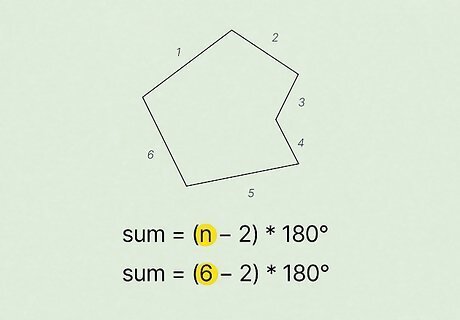
Plug the value of n {\displaystyle n} n into the formula. Remember, n {\displaystyle n} n is the number of sides in your polygon. For example, if you are working with a hexagon, n = 6 {\displaystyle n=6} n=6, since a hexagon has 6 sides. So, your formula should look like this: s u m = ( 6 − 2 ) × 180 {\displaystyle sum=(6-2)\times 180} sum=(6-2)\times 180

Solve for n {\displaystyle n} n. To do this, subtract 2 from the number of sides, and multiply the difference by 180. This will give you, in degrees, the sum of the interior angles in your polygon. For example, to find out the sum of the interior angles of a hexagon, you would calculate: s u m = ( 6 − 2 ) × 180 {\displaystyle sum=(6-2)\times 180} sum=(6-2)\times 180 s u m = ( 4 ) × 180 {\displaystyle sum=(4)\times 180} sum=(4)\times 180 s u m = ( 4 ) × 180 = 720 {\displaystyle sum=(4)\times 180=720} sum=(4)\times 180=720So, the sum of the interior angles of a hexagon is 720 degrees.

Drawing Triangles

Draw the polygon whose angles you need to sum. The polygon can have any number of sides and can be regular or irregular. For example, you might want to find the sum of the interior angles of a hexagon, so you would draw a six-sided shape.

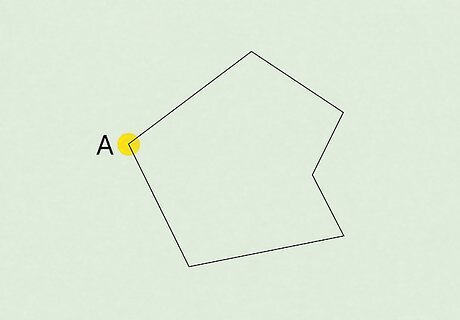
Choose one vertex. Label this vertex A. A vertex is a point where two sides of a polygon meet.

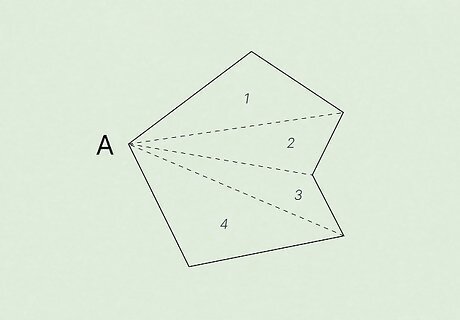
Draw a straight line from Point A to each other vertex in the polygon. The lines should not cross. You should create a number of triangles. You do not have to draw lines to the adjacent vertices, since they are already connected by a side. For example, for a hexagon you should draw three lines, dividing the shape into 4 triangles.

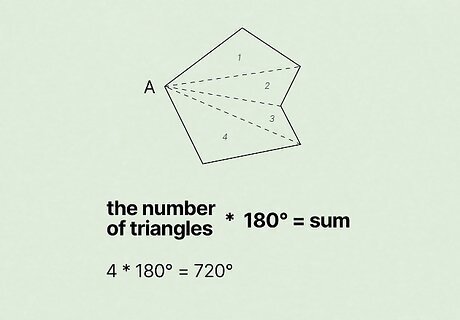
Multiply the number of triangles you created by 180. Since there are 180 degrees in a triangle, by multiplying the number of triangles in your polygon by 180, you can find the sum of the interior angles of your polygon. For example, since you divided your hexagon into 4 triangles, you would calculate 4 × 180 = 720 {\displaystyle 4\times 180=720} 4\times 180=720 to find a total of 720 degrees in the interior of your polygon.