How to Find the Perimeter of a Pentagon

Calculating Perimeter with Side Lengths

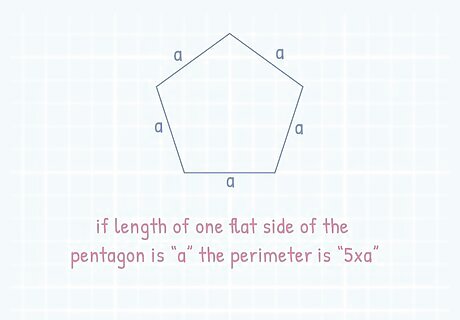
Identify the length of one flat side of the pentagon. The easiest way to find the perimeter of a pentagon is when the value of one side is already given to you. Each pentagon has five equal sides. If you are given the length of one side, it is easy to find the perimeter of the entire shape.

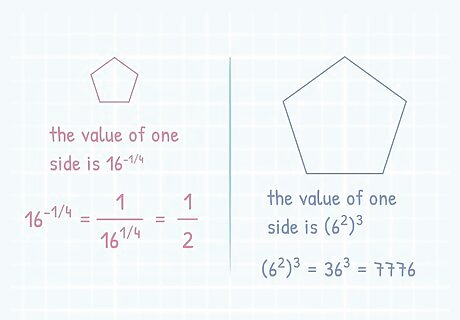
Solve the equation for the side length. If the side lengths are given as equations, you must solve them before finding the value of the pentagon’s perimeter. This will make it easier for you to find the perimeter more quickly. If the value of one side is 16 − 1 / 4 {\displaystyle 16^{-1/4}} {\displaystyle 16^{-1/4}}, then 16 − 1 / 4 {\displaystyle 16^{-1/4}} {\displaystyle 16^{-1/4}} must be simplified into 1 ( 16 1 / 4 ) {\displaystyle {\frac {1}{(16^{1/4})}}} {\displaystyle {\frac {1}{(16^{1/4})}}} 1 ( 16 1 / 4 ) {\displaystyle {\frac {1}{(16^{1/4})}}} {\displaystyle {\frac {1}{(16^{1/4})}}} = 1 16 4 {\displaystyle {\frac {1}{\sqrt[{4}]{16}}}} {\displaystyle {\frac {1}{\sqrt[{4}]{16}}}} which comes out to be 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}. If the value of one side is ( 6 2 ) 3 {\displaystyle (6^{2})^{3}} {\displaystyle (6^{2})^{3}}, simplify to 6 5 {\displaystyle 6^{5}} {\displaystyle 6^{5}} or 7776 {\displaystyle 7776} {\displaystyle 7776}.

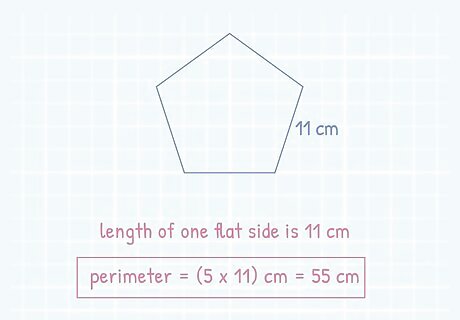
Multiply the value of one side by 5. If you know the length of one side of the pentagon, the next step is to multiply that value by 5. This represents the 5 sides of the shape that are all the same length. This is the simplest way to find the perimeter of the pentagon. If the value of one side is 11, then the equation would be 11 ∗ 5 {\displaystyle 11*5} {\displaystyle 11*5} which is 55 {\displaystyle 55} 55 The value of a polygon’s perimeter will always be positive. Depending on how large or complicated the value of one side is, you can calculate the perimeter of the pentagon using addition.

Solving for Perimeter with the Radius

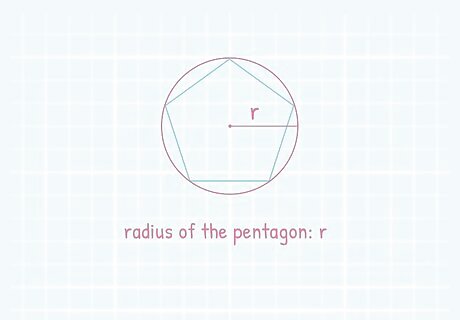
Locate the radius of the pentagon. The radius is a line drawn from the center of a shape to one of its vertices, also known as the circumradius. Pentagons have 5 vertices, or 5 points. For a pentagon, the radius would extend from the center of the shape out to one of the points. If you are given the radius of a pentagon, you can complete an equation that will give you the length of one of one side in order to calculate the perimeter. The value of a radius will always be positive.

Study the equation that uses radius to find the length of one side. The equation to find the length of one side of a pentagon using the radius looks like this: s i d e l e n g t h = 2 r s i n ( 180 n ) {\displaystyle sidelength=2rsin({\frac {180}{n}})} {\displaystyle sidelength=2rsin({\frac {180}{n}})}. It may look a little complicated, but you can easily plug in the numbers that you already know to simplify the equation and find the length of a side. r represents the radius of the pentagon. n is the number of sides the pentagon has. sin is a trigonometric function using degrees that is easily plugged into a calculator.

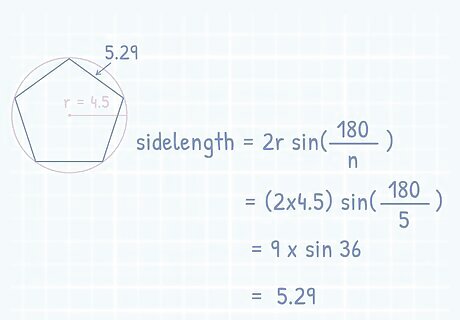
Plug the known values into the radius equation. Once you understand the equation to find side length using the radius of a pentagon, you can replace the letters with the numbers that you know. Replace the ‘n’ value with the number of sides (which for a pentagon is always 5) and the letter ‘r’ with the value given for the radius. If the radius is 4.5 {\displaystyle 4.5} {\displaystyle 4.5}, then 2 ( 4.5 ) ∗ s i n ( 180 5 ) {\displaystyle 2(4.5)*sin({\frac {180}{5}})} {\displaystyle 2(4.5)*sin({\frac {180}{5}})} would be your full equation. 2 ( 4.5 ) ∗ s i n ( 180 5 ) = 9 ∗ s i n ( 36 ) {\displaystyle 2(4.5)*sin({\frac {180}{5}})=9*sin(36)} {\displaystyle 2(4.5)*sin({\frac {180}{5}})=9*sin(36)} 9 ∗ s i n ( 36 ) = 5.29 {\displaystyle 9*sin(36)=5.29} {\displaystyle 9*sin(36)=5.29}

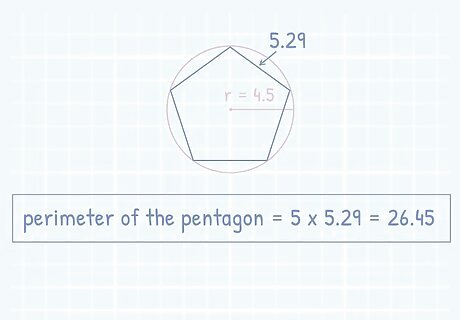
Multiply the answer by the number of sides. Once you have found the answer to the equation using the radius, solving for your final perimeter value is simple. To calculate the perimeter of the shape, multiply your answer to the equation by 5. 5.29 ∗ 5 = 26.45 {\displaystyle 5.29*5=26.45} {\displaystyle 5.29*5=26.45}

Using the Apothem to Find Perimeter

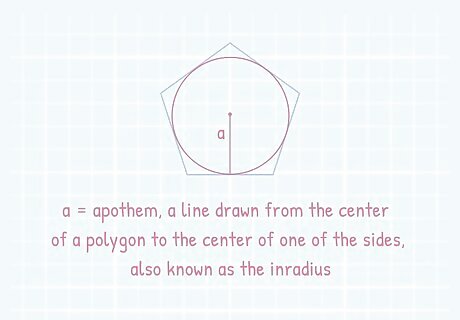
Locate the apothem of the pentagon. The apothem is a line drawn from the center of a polygon to the center of one of the sides, also known as the inradius. It is different than the radius which is drawn from the center of the polygon out to one of the vertices (or points). If you are given the apothem of a pentagon, there is another simple equation you can use to find the length of one side. The value of the apothem will always be positive.

Enter the known values into the apothem equation. Once you know the apothem, you can combine it with the number of sides (always 5 for a pentagon) into an equation to calculate the length of one side. The equation for finding the length of one side of a pentagon using the apothem is: s i d e l e n g t h = 2 a ∗ t a n ( 180 n ) {\displaystyle sidelength=2a*tan({\frac {180}{n}})} {\displaystyle sidelength=2a*tan({\frac {180}{n}})}. a represents the apothem value. n is the number of sides the pentagon has. tan is a tangent function that can be performed on a calculator using degrees.

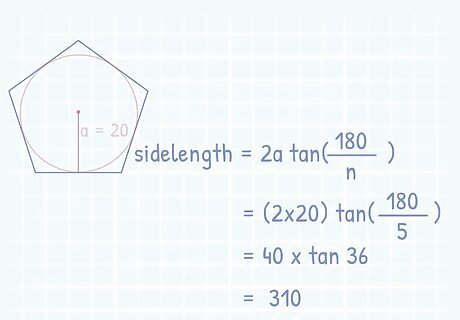
Solve the equation using the apothem value. Enter the value for the apothem into the equation for the letter ‘a’ and plug in the number of sides into the equation for the letter ‘n’. This will give you the value of one side of the polygon. If the value of the apothem is 20 {\displaystyle 20} 20, the equation would read s i d e l e n g t h = 2 ( 20 ) ∗ t a n ( 180 5 ) {\displaystyle sidelength=2(20)*tan({\frac {180}{5}})} {\displaystyle sidelength=2(20)*tan({\frac {180}{5}})}. s i d e l e n g t h = 40 ∗ t a n ( 36 ) {\displaystyle sidelength=40*tan(36)} {\displaystyle sidelength=40*tan(36)} which equals 310 {\displaystyle 310} {\displaystyle 310}.

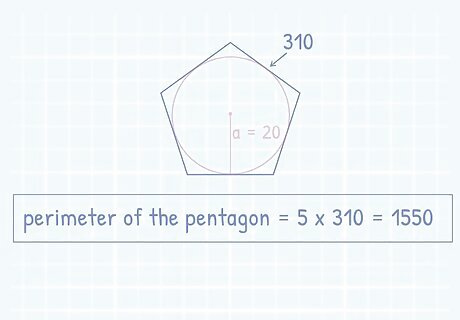
Calculate the final perimeter of the pentagon. Once you have figured out one side length using the apothem equation, you can find the perimeter of the pentagon by multiplying your answer by the number of sides in a pentagon. The equation you solved using the apothem gave you the value for one of the sides. Multiply your answer by 5. 310 ∗ 5 = 1550 {\displaystyle 310*5=1550} {\displaystyle 310*5=1550}.