
views
Problem Statement: Find the change in enthalpy needed to heat saturated liquid water at 0.1 MPa and 40°C to superheated steam at 0.3 MPa and 190°C.

Define what we are trying to find and label the given values. Enthalpy change is described as Δ H = H f i n a l − H i n i t i a l {\displaystyle \Delta H=H_{final}-H_{initial}} {\displaystyle \Delta H=H_{final}-H_{initial}}. T i n i t i a l {\displaystyle T_{initial}} {\displaystyle T_{initial}} = 40°C, T f i n a l {\displaystyle T_{final}} {\displaystyle T_{final}} = 190°C, P i n i t i a l {\displaystyle P_{initial}} {\displaystyle P_{initial}} = 0.1 MPa, P f i n a l {\displaystyle P_{final}} {\displaystyle P_{final}} = 0.3 MPa

Find the Steam Tables in the back of your textbook that have values for saturated water. Usually labeled Saturation Temperature and Saturation Pressure. (First page may look like the image below)

Locate the temperature 40°C in the left hand column of the table.

Follow it across the table to the enthalpy columns. Labeled HL, HVap or HV. We just know that our fluid is initially a liquid, so we will use the liquid enthalpy value, HL, as our initial enthalpy value. HL = 167.53 kJ/kg

Now locate the Superheated Steam table.

Identify the values relative to our final pressure (0.3 MPa)
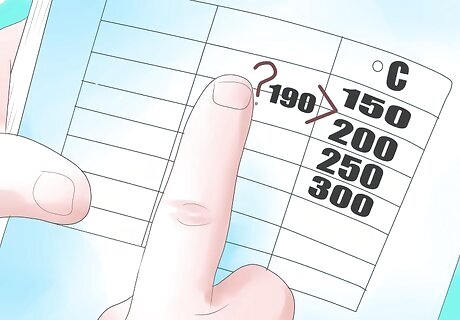
Locate our final temperature (190°C)

Recognize that 190 is not listed in the temperature column, therefore we must interpolate. Interpolating values gives us a best guess, when the desired temperature or pressure is between two available values. Interpolating follows the formula, HD (desired enthalpy) = [ ( H h i − H l o w ) / ( T h i − T l o w ) × ( T f i n a l − T l o w ) ] + H l o w {\displaystyle [(H_{hi}-H_{low})/(T_{hi}-T_{low})\times (T_{final}-T_{low})]+H_{low}} {\displaystyle [(H_{hi}-H_{low})/(T_{hi}-T_{low})\times (T_{final}-T_{low})]+H_{low}} For our example problem, T f i n a l {\displaystyle T_{final}} {\displaystyle T_{final}} = 190°C

Locate the temperature values just above and below 190°C, Thi and Tlow. In this case they are 200°C and 150°C.
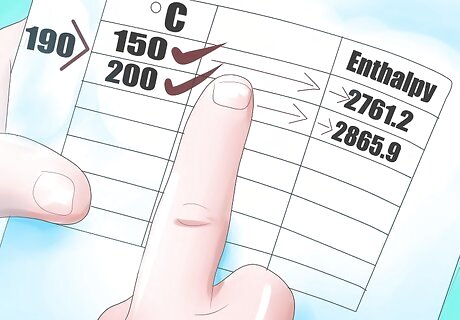
Now find the corresponding enthalpy values for 150°C and 200°C, Hhi and Hlow.

Follow the equation above to find the interpolated enthalpy value at 190°C.[(2865.9-2761.2)/(200-150)*(190-150)]+2761.2 H 190 {\displaystyle H_{190}} {\displaystyle H_{190}} = 2844.96 kJ/kg

Subtract our initial enthalpy value at 40°C ( 167.53 kJ/kg) from our final enthalpy value at 190°C (2844.96 kJ/kg), to find the change in enthalpy needed to heat water from its liquid phase to superheated steam. The answer is given below. ∆H = 2844.96 kJ/kg – 167.53 kJ/kg = 2677.43 kJ/kg



















Comments
0 comment