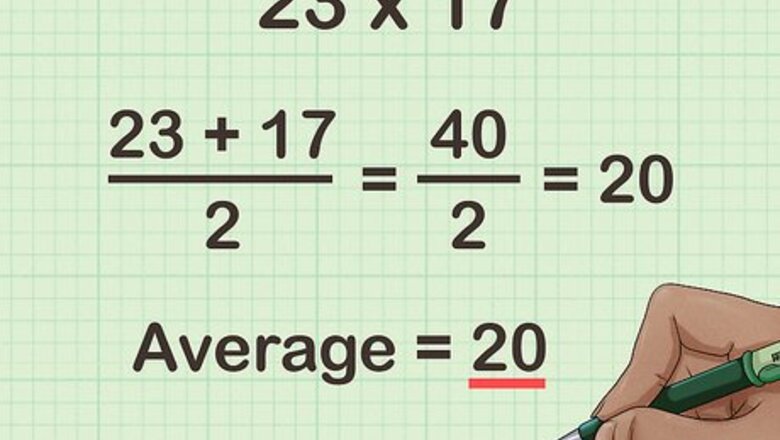
views
Finding the Difference of Two Squares
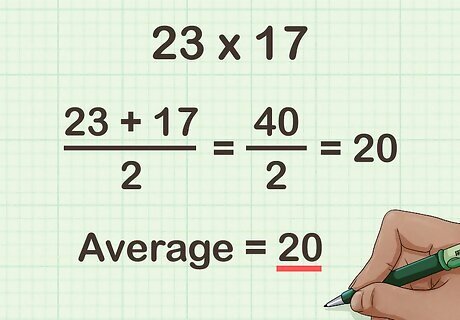
Find the average of the two factors you are multiplying. To find the average, add both numbers together, then divide by 2. You can also think of this as the number that both factors are equidistant from. Note that this method only works if the average of the two factors is a whole number. For example, if you are calculating 23 × 17 {\displaystyle 23\times 17} 23\times 17, find the average of 23 and 17: 23 + 17 2 = 40 2 = 20 {\displaystyle {\frac {23+17}{2}}={\frac {40}{2}}=20} {\frac {23+17}{2}}={\frac {40}{2}}=20So, the average is 20. In other words, 23 and 17 are equidistant from 20.
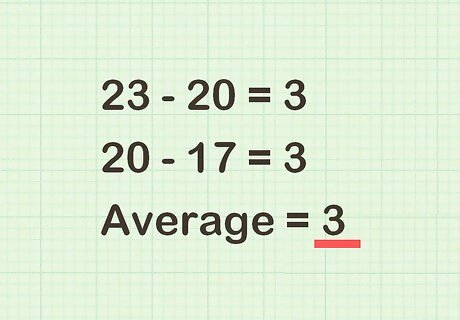
Find the difference between each factor and their average. This difference should be the same for both numbers. For example, since the average of 23 and 17 is 20, you would calculate 23 − 20 = 3 {\displaystyle 23-20=3} 23-20=3 and 20 − 17 = 3 {\displaystyle 20-17=3} 20-17=3. So, the difference between each factor and their average is 3.
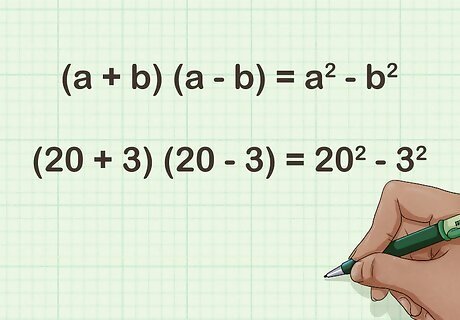
Recall the formula for the difference of two squares. The formula is ( a + b ) ( a − b ) = a 2 − b 2 {\displaystyle (a+b)(a-b)=a^{2}-b^{2}} (a+b)(a-b)=a^{{2}}-b^{{2}} For the purposes of multiplying two 2-digit numbers together, let a {\displaystyle a} a equal the average of the two products, and b {\displaystyle b} b equal the difference between each factor and their average. For example, ( 20 + 3 ) ( 20 − 3 ) = 20 2 − 3 2 {\displaystyle (20+3)(20-3)=20^{2}-3^{2}} (20+3)(20-3)=20^{{2}}-3^{{2}}.
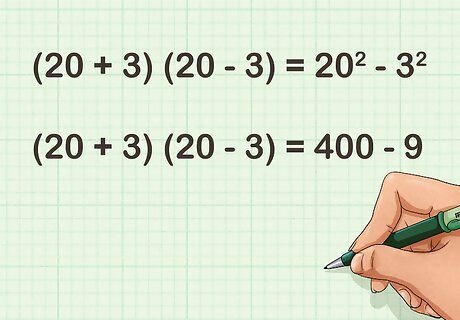
Square a {\displaystyle a} a and b {\displaystyle b} b. Remember that squaring a number means to multiply it by itself. Hopefully these numbers are easy for you to square in your head. If they aren’t, you might need to use another mental math method. For example: ( 20 + 3 ) ( 20 − 3 ) = 20 2 − 3 2 {\displaystyle (20+3)(20-3)=20^{2}-3^{2}} (20+3)(20-3)=20^{{2}}-3^{{2}} ( 20 + 3 ) ( 20 − 3 ) = 400 − 9 {\displaystyle (20+3)(20-3)=400-9} (20+3)(20-3)=400-9
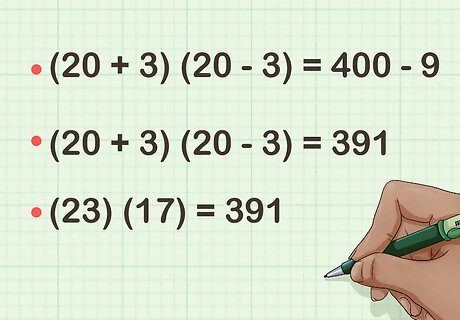
Calculate the difference between the two squares. The result will be the product of your original two factors. For example, ( 20 + 3 ) ( 20 − 3 ) = 391 {\displaystyle (20+3)(20-3)=391} (20+3)(20-3)=391. So, ( 23 ) ( 17 ) = 391 {\displaystyle (23)(17)=391} (23)(17)=391.
Using the Distributive Property

Determine which factor is closest to 100. This method works best when one of the factors is very close to 100, particularly when one of the factors is 99. But, this method may work for other factors as well. For example, you might be multiplying 12 × 98 {\displaystyle 12\times 98} 12\times 98. In this case, 98 is closest to 100.
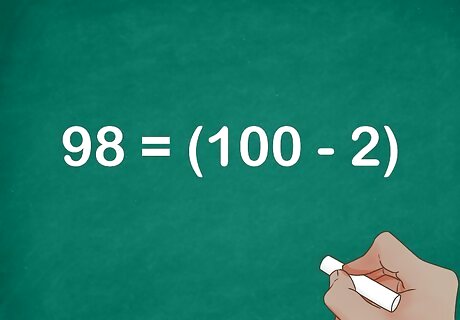
Re-express the factor closest to 100 as 100 − x {\displaystyle 100-x} 100-x. The variable x {\displaystyle x} x represents the difference between the factor and 100. For example, 98 = ( 100 − 2 ) {\displaystyle 98=(100-2)} 98=(100-2).
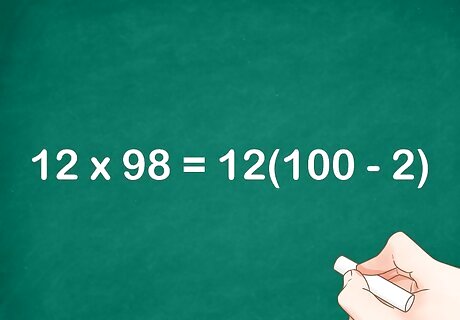
Substitute the re-expressed factor into the original equation. You should think about multiplying 100 − x {\displaystyle 100-x} 100-x by the smaller factor. For example, 12 × 98 = 12 ( 100 − 2 ) {\displaystyle 12\times 98=12(100-2)} 12\times 98=12(100-2).
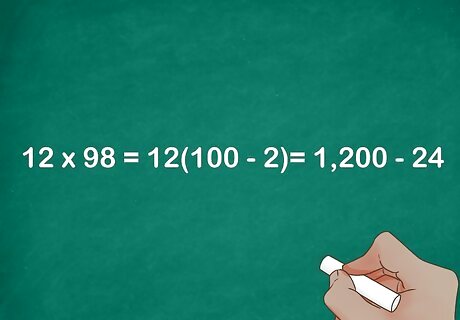
Multiply using the distributive property. Since the first number in parentheses is 100, it should be easy to find the first factor. Finding the second factor is easier the closest the original number is to 100. For example, 12 × 98 = 12 ( 100 − 2 ) = 1 , 200 − 24 {\displaystyle 12\times 98=12(100-2)=1,200-24} 12\times 98=12(100-2)=1,200-24. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher The distributive property helps you avoid repetitive calculations. You can use the distributive property to solve equations where you must multiply a number by a sum or difference. It simplifies calculations, enables expression manipulation (like factoring), and forms the basis for solving many equations.
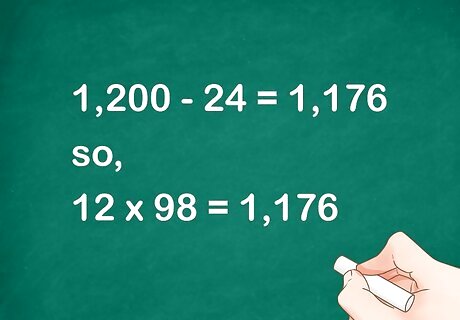
Find the difference between the two products. This will give you the product of your original two factors. For example, 1 , 200 − 24 = 1 , 176 {\displaystyle 1,200-24=1,176} 1,200-24=1,176, so 12 × 98 = 1 , 176 {\displaystyle 12\times 98=1,176} 12\times 98=1,176.
Doubling and Halving
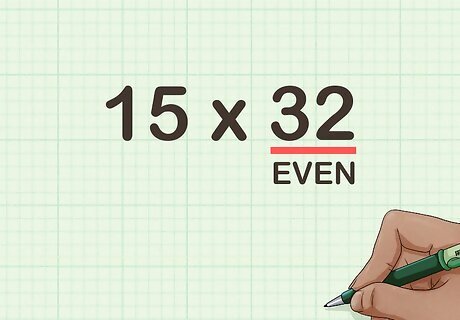
Determine whether either factor is even. You will be halving the even number. Remember that an even number is one that is divisible by 2. If both factors are even, choose the smaller number to halve. For example, if you are multiplying 15 × 32 {\displaystyle 15\times 32} 15\times 32, you would halve the 32, since it is an even number.
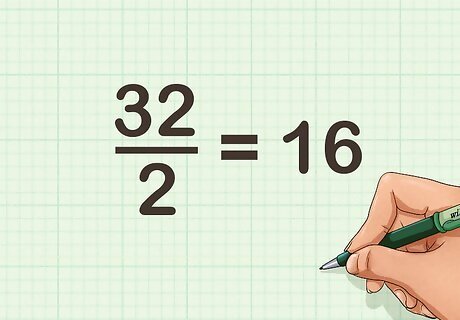
Half the even number. To do this, divide by 2. If you know your math facts well, you should be able to do this easily. For example, 32 2 = 16 {\displaystyle {\frac {32}{2}}=16} {\frac {32}{2}}=16.
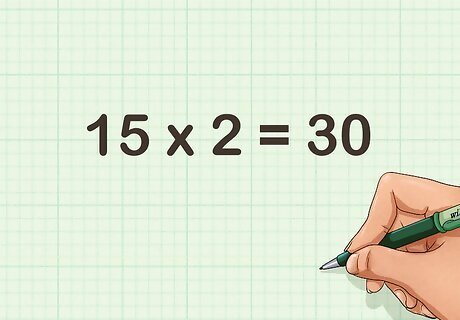
Double the other number. To double a number, multiply it by 2. For example, 15 × 2 = 30 {\displaystyle 15\times 2=30} 15\times 2=30.
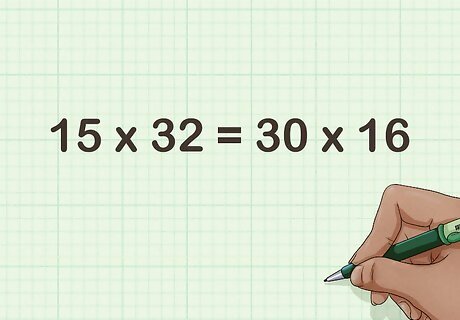
Consider the new multiplication problem. The new problem is the result of halving one of the factors and doubling the other. For example, 15 × 32 = 30 × 16 {\displaystyle 15\times 32=30\times 16} 15\times 32=30\times 16.
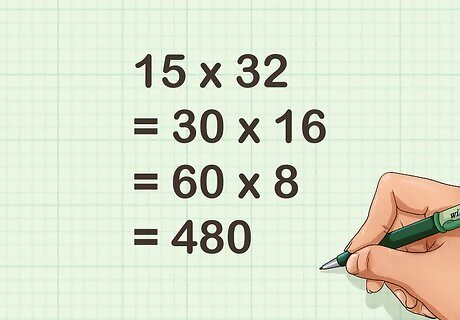
Continue the process until you arrive at a problem you can compute mentally. Make sure you always halve the same number, and double the same number. The amount of times you halve and double should be same for both factors. For example: 15 × 32 {\displaystyle 15\times 32} 15\times 32 = 30 × 16 {\displaystyle =30\times 16} =30\times 16 = 60 × 8 {\displaystyle =60\times 8} =60\times 8 = 480 {\displaystyle =480} =480


















Comments
0 comment