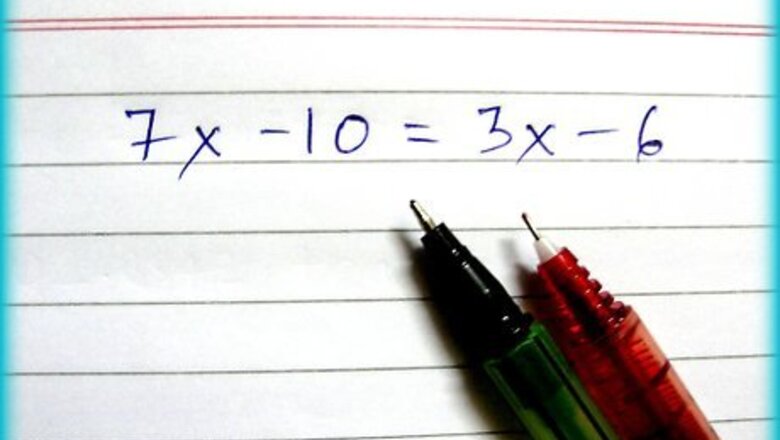
views
x
{\displaystyle x}
equals if you have a problem like
7
x
−
10
=
3
x
+
6
{\displaystyle 7x-10=3x+6}
. This kind of equation is called a linear equation,[1]
X
Research source
and it usually has just one variable. This article will walk you through the simple steps.
Starting with the Variables on Opposite Sides

Look at your problem. A simple linear equation might look like 7 x − 10 = 3 x − 6 {\displaystyle 7x-10=3x-6} 7x-10=3x-6.

Check the equation for varying terms and constant terms. Varying terms are numbers like 7 x {\displaystyle 7x} 7x, 3 x {\displaystyle 3x} 3x, 6 y {\displaystyle 6y} 6y or 10 z {\displaystyle 10z} 10z, where the number changes depending on what you plug into the variable, or letter. Constant terms are numbers like 10 {\displaystyle 10} 10, 6 {\displaystyle 6} 6 or 30 {\displaystyle 30} 30, where the number never changes. Usually, equations won't come with varying terms and constant terms lined up on separate sides. In the example above, the left-hand side (LHS) has both varying and constant terms, as does the right-hand side (RHS).

Prepare to move the numbers around so that the varying terms are on one side and the constant terms are on the side such as in 16 x − 5 x = 32 − 10 {\displaystyle 16x-5x=32-10} 16x-5x=32-10 (that equation is solved in example 2). In order to do this, you may have to subtract or add the numbers you want to move from both sides. In the next step, you'll see how to do that in example 1. The equation 16 x − 5 x = 32 − 10 {\displaystyle 16x-5x=32-10} 16x-5x=32-10 does have all the varying terms on one side (LHS), while all the constant terms are on the other side (RHS).
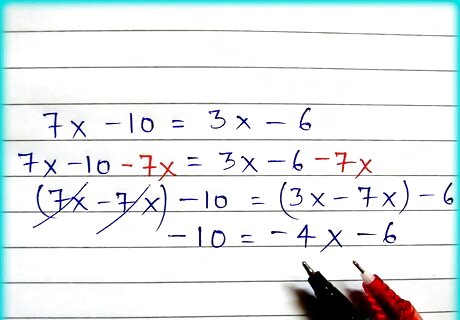
Move the varying terms to one side of the equation. It doesn't matter to which side you move the varying terms. In example 1, 7 x − 10 = 3 x − 6 {\displaystyle 7x-10=3x-6} 7x-10=3x-6 can be rearranged by choosing to subtract either 7 x {\displaystyle 7x} 7x or 3 x {\displaystyle 3x} 3x from both sides. Choosing to subtract 7 x {\displaystyle 7x} 7x, you have: ( 7 x − 7 x ) − 10 = ( 3 x − 7 x ) − 6 − 10 = − 4 x − 6 {\displaystyle {\begin{aligned}(7x-7x)-10&=(3x-7x)-6\\-10&=-4x-6\end{aligned}}} {\begin{aligned}(7x-7x)-10&=(3x-7x)-6\\-10&=-4x-6\end{aligned}}
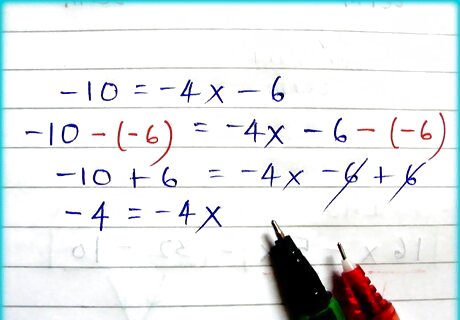
Bring all the constant terms onto the other side of the equation. That is: move the constant terms so that they are on the opposite side of the equation from where the varying terms are. We see that − 6 {\displaystyle -6} -6 must be subtracted from both sides: − 10 − ( − 6 ) = − 4 x − 6 − ( − 6 ) − 4 = − 4 x {\displaystyle {\begin{aligned}-10-(-6)&=-4x-6-(-6)\\-4&=-4x\end{aligned}}} {\begin{aligned}-10-(-6)&=-4x-6-(-6)\\-4&=-4x\end{aligned}}

Divide both sides by the coefficient of x {\displaystyle x} x. The coefficient of x {\displaystyle x} x (or y {\displaystyle y} y, or z {\displaystyle z} z, or any letter) is the number in front of the varying term. The coefficient of x {\displaystyle x} x in − 4 x {\displaystyle -4x} -4x is − 4 {\displaystyle -4} -4. So divide both sides by − 4 {\displaystyle -4} -4 to get the value of x = 1 {\displaystyle x=1} x=1. Our answer to the equation 7 x − 10 = 3 x − 6 {\displaystyle 7x-10=3x-6} 7x-10=3x-6 is x = 1 {\displaystyle x=1} x=1. You can check this answer by plugging 1 {\displaystyle 1} 1 back into every x {\displaystyle x} x variable and seeing if both sides of the equation equal the same number: 7 ( 1 ) − 10 = 3 ( 1 ) − 6 − 3 = − 3 {\displaystyle {\begin{aligned}7(1)-10&=3(1)-6\\-3&=-3\end{aligned}}} {\begin{aligned}7(1)-10&=3(1)-6\\-3&=-3\end{aligned}}
Starting with the Variables on One Side
Know that sometimes the varying terms and the constant terms will be separate. Sometimes, half of your work will be done for you. You'll have all the varying terms on one side and all the constant terms on the other side. If this is the case, all you have to do is the following.

Simplify both sides. For the equation 16 x − 5 x = 32 − 10 {\displaystyle 16x-5x=32-10} 16x-5x=32-10, we just have to subtract the numbers from one another.
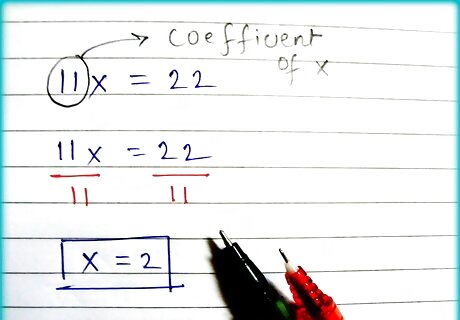
Next, divide both sides by the coefficient of x {\displaystyle x} x. Remember that the coefficient of x is the number in front of the varying term. In this example, the coefficient of x {\displaystyle x} x in 11 x {\displaystyle 11x} 11x is 11 {\displaystyle 11} 11. That division is 11 x / 11 = 22 / 11 {\displaystyle 11x/11=22/11} 11x/11=22/11 to get x = 2 {\displaystyle x=2} x=2. The answer to the equation 16 x − 5 x = 32 − 10 {\displaystyle 16x-5x=32-10} 16x-5x=32-10 is x = 2 {\displaystyle x=2} x=2.

















Comments
0 comment