views
Quickly Comprehending Your Loan
Input your loan information into an online calculator to quickly determine your interest payments. Calculating interest payments is not a simple equation. Luckily, a quick search for "interest payment calculator" makes it easy to find your payment amounts as long as you know what to input into the calculator: Principal: The amount of your loan. If you loan is $5,000, the principal is $5,000. Interest: In simple terms, the percentage of money you're being charged to have the loan. It is either given as a percentage (such as 4%) or a decimal (.04). Term: Usually in months, this is how long you have to pay the loan off. For mortgages it is often calculated in years. Make sure to find out if there are any penalties for paying off the loan earlier than the stated term. Payment Option: Almost always a "fixed-term loan." However this can be different for specialty loans. Ask if the interest and payment schedule is fixed before getting a loan if you are unsure.

Find out your interest rate before getting a loan. The interest rate is the cost you pay for borrowing money. It is the rate of interest that you will pay on the principal for the life of the loan. You want it to be as low as possible, as even .5% of a difference can mean a huge sum of money. If you would prefer lower payments, you may pay a higher interest rate and more total interest over the loan, but less each month. Someone with less savings on hand or whose income is bonus or commission-based would likely prefer this option. However, want to stay below 10% interest whenever possible. The common rates for different loans are: Auto: 4-7% Home: 3-6% Personal Loans: 5-9% Credit Cards: 18-22% This is why you should avoid large purchases you can't repay quickly on credit cards. Payday Loans: 350-500% These loans are very dangerous if you can't pay them off within 1-2 weeks. These loans are regulated by the state, which means that some of them have caps on the interest they can charge while others do not have a limit.

Ask about accrual rates to determine when you get charged interest. In technical terms, the accrual rate tells you how often lender calculates the interest you owe. The more frequently you're charged the more you owe, since you have less time to pay off and the bill and prevent higher interest. Look, for example, at a $100,000 loan with 4% interest, compounded three different ways: Yearly: $110,412.17 Monthly: $110,512.24 Daily: $110,521.28 EXPERT TIP Paridhi Jain Paridhi Jain Certified Public Accountant Paridhi Jain is a Certified Public Accountant and the Co-Founder of Seva Ltd, a CPA firm operating in Maryland and Alabama. She has over 10 years of professional experience in the financial sector and has built a reputation for assisting small business owners navigate the intricacies of regulatory compliance, encompassing areas from company structuring and entity formation to detailed nexus determinations for income and sales tax. She is an active member of the Alabama Society of CPAs and has a certification in pre-professional accounting. She graduated Magna Cum Laude from the University of Maryland, Baltimore County with a major in Information Systems. Paridhi Jain Paridhi Jain Certified Public Accountant Knowing loan interest costs daily clarifies budget decisions. Figuring out the daily interest costs makes loan details way clearer. Just take the yearly percent rate and divide by the total days in a year. Say a $100 loan has 10% yearly interest — that's around 2.7 cents per day. Knowing the daily cost helps decide if a loan works for your budget or not.

Use longer term loans to pay less each month, but more overall. The term is the period of time that you have to repay the loan. Again, this will vary from one loan to the next, and you'll need to choose a loan with a term that meets your needs. If you are unsure about taking a shorter term loan with higher payments, then you can also always take out a longer term loan and pay a little more on the principal each month to cut back on the interest. A longer term will typically result in more interest paid over the life the loan, but smaller monthly payments. For example, say you have a $20,000 auto loan with 5% interest. Total payment would be: 24 Month Term: You pay $1,058.27 in total interest, but only $877.43 each month. 30 Month Term: You pay $1,317.63 in total interest, but only $710.59 each month. 36 Month Term: You pay $1,579.02 in total interest, but only $599.42 each month.
Calculating your Payment by Hand

Learn the formula for complex interest payments. Despite all of the online calculators available for calculating payments and interest, understanding how interest and payments are calculated is essential for making an informed decision on your loans. Calculating your payments and interest requires the use of a mathematical formula, which is as follows: P a y m e n t = P r i n c i p a l ∗ i ( 1 + i ) n ( 1 + i ) n − 1 {\displaystyle Payment=Principal*{\frac {i(1+i)^{n}}{(1+i)^{n}-1}}} Payment=Principal*{\frac {i(1+i)^{n}}{(1+i)^{n}-1}} The "i" represents interest rate, and the "n" represents the number of payments. Like most equations in finance, the formula for determining your payment is much more intimidating than the math itself. Once you understand how to set up the numbers, calculating your monthly payment is as easy as pie.

Adjust for frequency of payments. Before you plug numbers into the equation, you must adjust your interest payment “i” for how often you are paying. For example, imagine you took out a loan at 4.5 percent, and the loan required you to make payments on a monthly basis. Since your payments are monthly, you will need to divide the interest rate by 12. 4.5 percent (.045) divided by 12 equals 0.00375. Plug this number in for "i."

Adjust for number of payments. To determine what to plug in for "n," your next step is to determine the total number of payments you'll be making over the term of the loan. Imagine that your monthly payments are on a loan with a 30 year term. To find the number of payments, simply multiply 30 by 12. You'll be making 360 payments.

Calculate your monthly payment. To figure your monthly payment on this loan, it is now just a matter of plugging the numbers into the formula. This might look intimidating, but if you go step by step, you'll soon have your interest payment. Below are the steps of the calculation, done one by one. Continuing with the example above, imagine you have borrowed $100,000. Your equation will look like this: 100 , 000 ∗ 0.00375 ( 1 + 0.00375 ) 3 60 ( 1 + 0.00375 ) 3 60 − 1 {\displaystyle 100,000*{\frac {0.00375(1+0.00375)^{3}60}{(1+0.00375)^{3}60-1}}} 100,000*{\frac {0.00375(1+0.00375)^{3}60}{(1+0.00375)^{3}60-1}} 100 , 000 ∗ 0.00375 ( 1.00375 ) 3 60 ( 1 + 0.00375 ) 3 60 − 1 {\displaystyle 100,000*{\frac {0.00375(1.00375)^{3}60}{(1+0.00375)^{3}60-1}}} 100,000*{\frac {0.00375(1.00375)^{3}60}{(1+0.00375)^{3}60-1}} 100 , 000 ∗ 0.00375 ( 3.84769.... ) ( 1 + 0.00375 ) 3 60 − 1 {\displaystyle 100,000*{\frac {0.00375(3.84769....)}{(1+0.00375)^{3}60-1}}} 100,000*{\frac {0.00375(3.84769....)}{(1+0.00375)^{3}60-1}} 100 , 000 ∗ 0.01442..... ( 1 + 0.00375 ) 3 60 − 1 {\displaystyle 100,000*{\frac {0.01442.....}{(1+0.00375)^{3}60-1}}} 100,000*{\frac {0.01442.....}{(1+0.00375)^{3}60-1}} 100 , 000 ∗ 0.01442..... ( 1.00375 ) 3 60 − 1 {\displaystyle 100,000*{\frac {0.01442.....}{(1.00375)^{3}60-1}}} 100,000*{\frac {0.01442.....}{(1.00375)^{3}60-1}} 100 , 000 ∗ 0.01442..... 3.84769..... − 1 {\displaystyle 100,000*{\frac {0.01442.....}{3.84769.....-1}}} 100,000*{\frac {0.01442.....}{3.84769.....-1}} 100 , 000 ∗ 0.01442..... 2.84769..... {\displaystyle 100,000*{\frac {0.01442.....}{2.84769.....}}} 100,000*{\frac {0.01442.....}{2.84769.....}} 100 , 000 ∗ 0.00506685..... = 506.69 {\displaystyle 100,000*0.00506685.....=506.69} 100,000*0.00506685.....=506.69 $506.69. This will be your monthly payment.
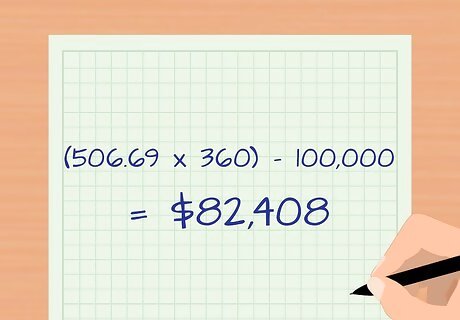
Calculate your total interest. Now that you have the monthly payment, you can determine how much interest you will pay over the life of the loan. Multiply the number of payments over the life of the loan by your monthly payment. Then subtract the principal amount you borrowed. Using the example above, you'd multiply $506.69 by 360 and get $182,408. This is the total amount you'll pay over the loan's term. Subtract $100,000 and you end up with $82,408. That is the total amount of interest you'd pay on this loan.
Calculating your Interest with Excel
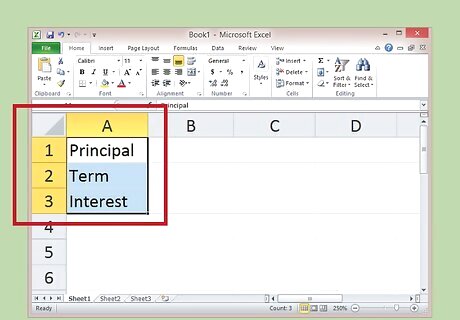
Write down the principal, term ,and interest from your loan in one column. Fill separate boxes with the amount of the loan, the length you have to pay, and the interest, and Excel can calculate your monthly payments for you. For the remainder of the section, you can use the following example loan: You take out a $100,000 home loan. You have 30 years to pay it off at 4.5% annual interest rate.
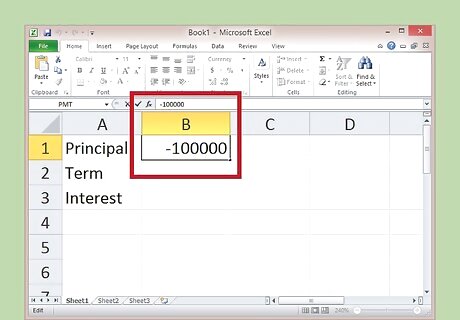
Write the principal in as a negative number. You need to tell Excel that you're paying a debt. To do so, write the principal with a negative number, without the $ sign. -100,000 = Principal
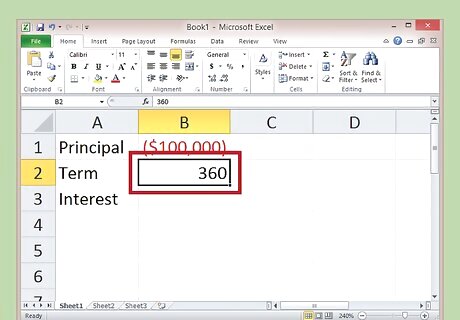
Determine the number of payments you're making. You can leave it in years, if you want, but your answer would spit out yearly interest payments, not monthly. Since most loans are paid monthly, simply multiple the number of years by 12 to get your total number of payments. Write this down in another box. -100,000 = Principal 360 = Number of Payments
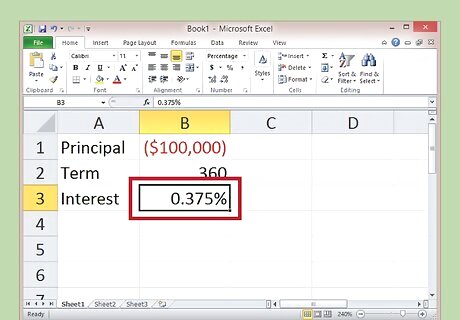
Convert your interest rate to fit the number of payments. In this example, your interest rate is annual, meaning it is calculated at the end of the year. However, you're paying monthly, meaning you need to know what your monthly interest rate is. Since 4.5% is for 12-months of interest, simply divide by 12 to get one month's worth of interest. Be sure to convert the percentage to a decimal when you're done. -100,000 = Principal 360 = Number of Payments 4.5 % 12 = .375 % = {\displaystyle {\frac {4.5\%}{12}}=.375\%=} {\frac {4.5\%}{12}}=.375\%= .00375 {\displaystyle .00375} .00375 = Monthly interest.
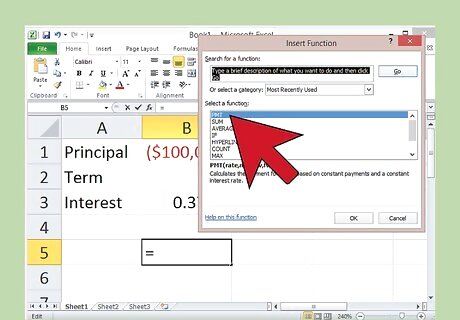
Use the =PMT function to determine interest payments. Excel already knows the equation for calculating monthly payments, with interest. You just have to give it the information it needs to make the calculation. Click on an empty box, then locate the function bar. It is located right above the spreadsheet and labeled "fx." Click inside of it and write "=PMT(" Do not include the quotation marks. If you're Excel savvy, you can set up Excel to accept the payment values for you.
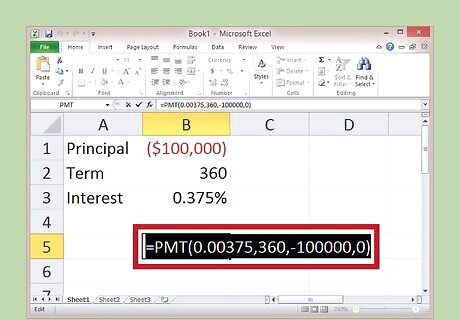
Enter the inputs in the correct order. Place the values needed to calculate the payment in the parenthesis, separated by commas. In this case, you'll enter (Interest rate,number of periods,principal ,0). Using the example above, the full entry should read: "=PMT(0.00375,360,-100000,0)" The last number is a zero. The zero indicates you will have a balance of $0 at the end of your 360 payments. Make sure you remember to close the parenthesis off.
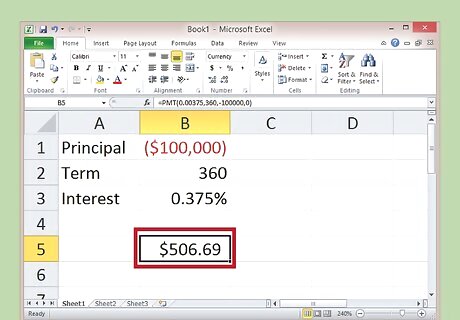
Press enter to get your monthly payment. If you've entered the function correctly, you should see your total monthly payment in =PMT cell of the spreadsheet. In this case, you'll see the number $506.69. That will be your monthly payment. If you see "#NUM!" or some other output that doesn't make sense to you in cell, you've entered something incorrectly. Double check the text in the function bar and try again.
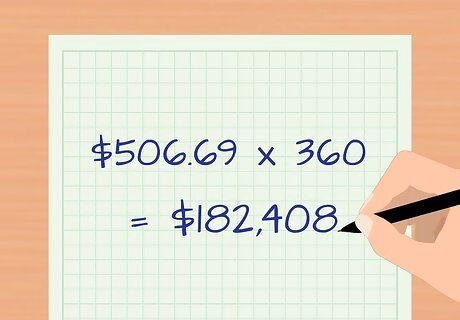
Figure out the total payment amount by multiplying by your number of payments. To figure out the total amount you will pay over the life of your loan, all you have to do is multiply the payment amount by the total number of payments. In the example, you'd multiply $506.69 by 360 to get $182,408. This is the total amount you'll pay over the loan's term.
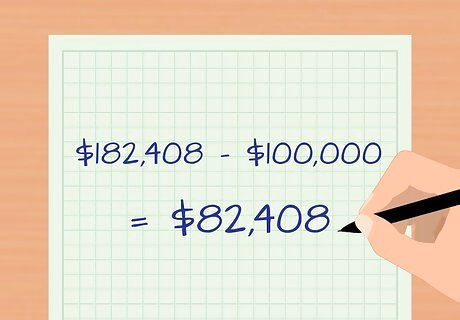
Figure out how much you pay in interest by subtracting the principal from your total. If you want to know how much interest you'll pay over the term of the loan, this is just a matter of subtraction. Subtract the principal from the total amount you'll pay. In the example you'd subtract $100,000 from $182,408. You end up with $82,408. This is your total interest paid.




















Comments
0 comment