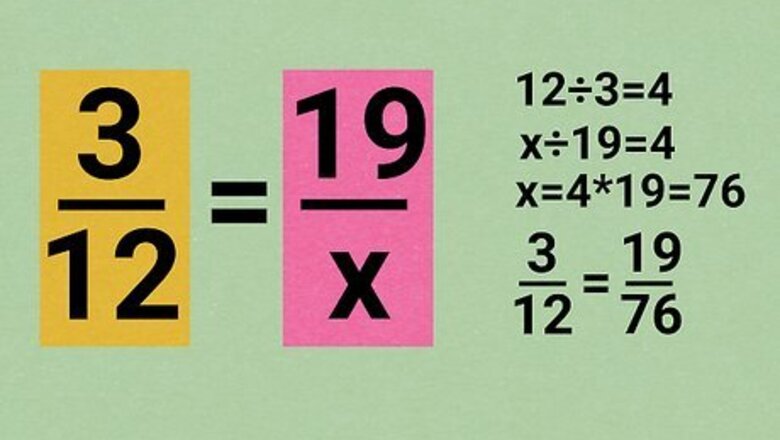
views
1
2
{\displaystyle {\frac {1}{2}}}
. A proportion is a pair of fractions that are equal to each other, like
1
2
=
2
4
{\displaystyle {\frac {1}{2}}={\frac {2}{4}}}
. There are many different ways to solve proportion problems that ask you to find the missing number
x
{\displaystyle x}
, and you don't need to learn all of them today. If you're learning pre-algebra and are just starting to use proportions, read from the top until you find a method that makes sense to you. If you're taking algebra and are working on more advanced proportions problems, you might need to skip down to later methods.
What is the "vertical" way to solve a proportion?
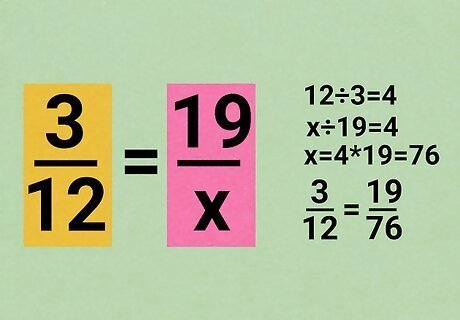
Use the relationship between the top and bottom number of the fraction. If you can multiply or divide the top number to get the bottom number, this method is the easiest. 3 12 = 19 x {\displaystyle {\frac {\color {blue}{3}}{\color {blue}{12}}}={\frac {19}{x}}} {\displaystyle {\frac {\color {blue}{3}}{\color {blue}{12}}}={\frac {19}{x}}} How are 3 and 12 related? 3 × 4 = 12 {\displaystyle 3\times {\textbf {4}}=12} {\displaystyle 3\times {\textbf {4}}=12} The other vertical column is related the same way: 19 × 4 = x {\displaystyle 19\times {\textbf {4}}=x} {\displaystyle 19\times {\textbf {4}}=x} x = 76 {\displaystyle x=76} {\displaystyle x=76}, so 3 12 = 19 76 {\displaystyle {\frac {3}{12}}={\frac {19}{76}}} {\displaystyle {\frac {3}{12}}={\frac {19}{76}}}
How can I solve a proportion with the "horizontal" method?
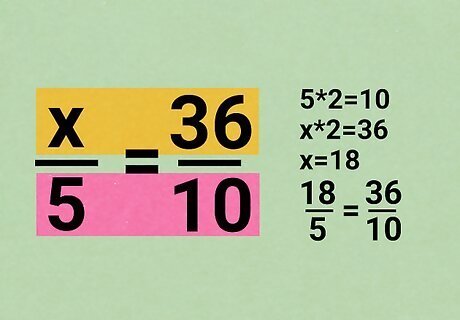
Use the relationship between the two numbers across the proportion. You can also look from left to right, across the two fractions: x 5 = 36 10 {\displaystyle {\frac {x}{\color {orange}{5}}}={\frac {36}{\color {orange}{10}}}} {\displaystyle {\frac {x}{\color {orange}{5}}}={\frac {36}{\color {orange}{10}}}} What is the relationship between 5 and 10? 5 × 2 = 10 {\displaystyle 5\times {\textbf {2}}=10} {\displaystyle 5\times {\textbf {2}}=10} The other horizontal row is related the same way: x × 2 = 36 {\displaystyle x\times {\textbf {2}}=36} {\displaystyle x\times {\textbf {2}}=36} x = 18 {\displaystyle x=18} {\displaystyle x=18}, so 18 5 = 36 10 {\displaystyle {\frac {18}{5}}={\frac {36}{10}}} {\displaystyle {\frac {18}{5}}={\frac {36}{10}}}
How do I solve a proportion step by step by cross-multiplying?
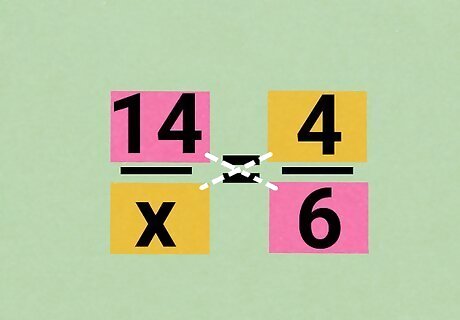
Draw two diagonal lines in an "X" across the proportion. For example, write down this proportion, then draw one line between the purple terms, and another line between the green terms: 14 x = 4 6 {\displaystyle {\frac {\color {purple}{14}}{\color {green}{x}}}={\frac {\color {green}{4}}{\color {purple}{6}}}} {\displaystyle {\frac {\color {purple}{14}}{\color {green}{x}}}={\frac {\color {green}{4}}{\color {purple}{6}}}}
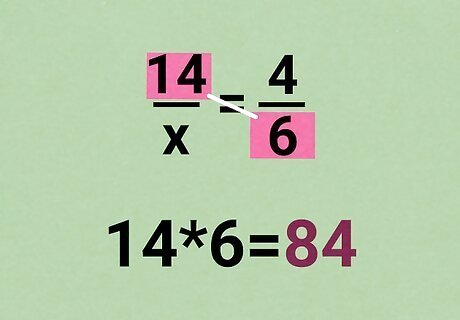
Multiply the two numbers connected by a line. One of the lines will connect two numbers (instead of a number and a variable like x {\displaystyle x} x). Find the product of these two numbers: 14 × 6 = 84 {\displaystyle \color {purple}{14\times 6}\color {black}{=}84} {\displaystyle \color {purple}{14\times 6}\color {black}{=}84}
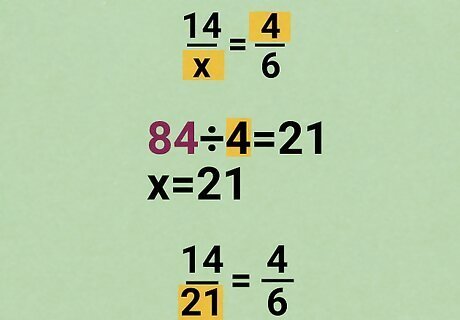
Divide by the last number in the proportion. Take the answer to your multiplication problem and divide it by the number you haven't used yet. (This is the green number in the example.) The result is the value of x {\displaystyle x} x, the missing number in your proportion. 84 ÷ 4 = 21 {\displaystyle \color {purple}{84}\color {black}{\div }\color {green}{4}\color {black}{=21}} {\displaystyle \color {purple}{84}\color {black}{\div }\color {green}{4}\color {black}{=21}} x = 21 {\displaystyle x=21} {\displaystyle x=21}, so you can fill in your proportion like this: 14 21 = 4 6 {\displaystyle {\frac {14}{21}}={\frac {4}{6}}} {\displaystyle {\frac {14}{21}}={\frac {4}{6}}}
How do you find the missing value in a proportion with a table of ratios?
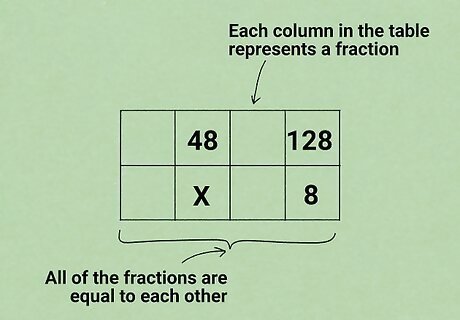
Draw a table with two rows. Put the top numbers in your proportion in the top row, and the bottom numbers in the second row. Keep numbers in the same fraction in the same column, and leave a few empty columns between them and to either side. Here's an example for the problem 48 x = 128 8 {\displaystyle {\bf {{\frac {48}{x}}={\frac {128}{8}}}}} {\displaystyle {\bf {{\frac {48}{x}}={\frac {128}{8}}}}}: 48 128 x 8 Each column in this table represents a fraction. All of the fractions in this table are equal to each other.
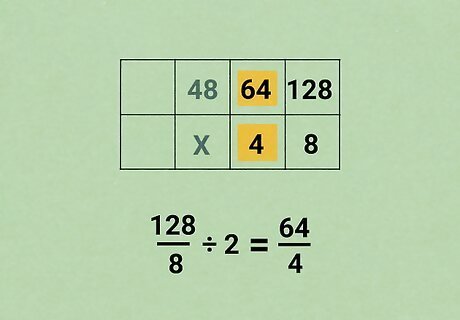
Add equivalent fractions to your table. Start with the fraction where you know both numbers, then multiply or divide each number in that column by the same amount. Write the new fraction into your table, putting it in a column so that the numbers are in order: For example, try dividing the top and bottom of 128 8 {\displaystyle {\frac {128}{8}}} {\displaystyle {\frac {128}{8}}} by 2. This gives you a new fraction, 64 4 {\displaystyle {\frac {64}{4}}} {\displaystyle {\frac {64}{4}}}, to put in your table. 48 64 128 x 4 8
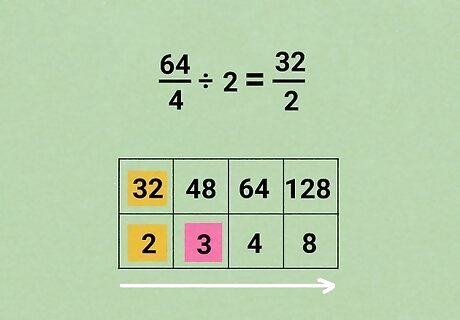
Repeat until you notice the pattern. As you find new fractions, make sure to put them in the table so that the numbers are in order. This will help you narrow down options for the value of x. Both the top and bottom of 64 4 {\displaystyle {\frac {64}{4}}} {\displaystyle {\frac {64}{4}}} are divisible by 2 again, giving you the fraction 32 2 {\displaystyle {\frac {32}{2}}} {\displaystyle {\frac {32}{2}}}. 32 48 64 128 2 x 4 8 The x in your table is somewhere between 2 and 4. Let's try 3 by plugging it back into your proportion: 48 3 = 128 8 {\displaystyle {\frac {48}{\bf {3}}}={\frac {128}{8}}} {\displaystyle {\frac {48}{\bf {3}}}={\frac {128}{8}}}
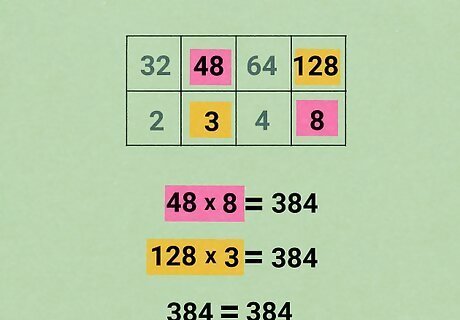
Check your work. Always check your work with this method. Sometimes the answer won't be a whole number, and you'll have to add fractions to your table or use a different method. To check whether 48 3 = 128 8 {\displaystyle {\frac {48}{3}}={\frac {128}{8}}} {\displaystyle {\frac {48}{3}}={\frac {128}{8}}} is the correct solution, draw two diagonal lines across the fraction. Multiply the two numbers along one line: 48 × 8 = 384 {\displaystyle 48\times 8=384} {\displaystyle 48\times 8=384}. Now multiply the two numbers along the other line: 3 × 128 = 384 {\displaystyle 3\times 128=384} {\displaystyle 3\times 128=384}. The two answers are the same, which means your answer is correct.
How do you solve percent proportions?

Rewrite the problem as a proportion. You can write any percentage as a fraction of 100. Use this fact to set up a problem as a proportion (two equal fractions): The proportion will always follow the form P a r t W h o l e = % 100 {\displaystyle {\frac {Part}{Whole}}={\frac {\%}{100}}} {\displaystyle {\frac {Part}{Whole}}={\frac {\%}{100}}}. For word problems, the "part" usually appears next to the word "is", and the "whole" usually comes after the word "of". For example, "3 is what percentage of 6?" can be rewritten as 3 6 = x 100 {\displaystyle {\frac {3}{6}}={\frac {x}{100}}} {\displaystyle {\frac {3}{6}}={\frac {x}{100}}}. The percentage is unknown, so we write it as x {\displaystyle x} x and solve for it.
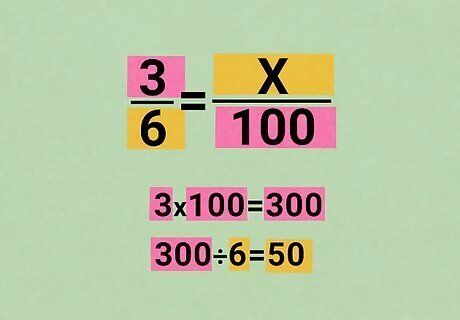
Solve by cross-multiplying or any other method. Now that it's set up as a proportion, you can solve the problem by any method. One of the most common methods is cross-multiplication: First multiply across the diagonal line with two known numbers. For the proportion 3 6 = x 100 {\displaystyle {\frac {\color {purple}{3}}{6}}={\frac {x}{\color {purple}{100}}}} {\displaystyle {\frac {\color {purple}{3}}{6}}={\frac {x}{\color {purple}{100}}}}, that means multiplying 3 × 100 = 300 {\displaystyle 3\times 100=300} {\displaystyle 3\times 100=300}. Now divide your answer by the last remaining number in the proportion: 300 ÷ 6 = 50 {\displaystyle 300\div 6=50} {\displaystyle 300\div 6=50}. x = 50 {\displaystyle x=50} {\displaystyle x=50} and the complete proportion is 3 6 = 50 100 {\displaystyle {\frac {3}{6}}={\frac {50}{100}}} {\displaystyle {\frac {3}{6}}={\frac {50}{100}}}
How do you solve proportions algebraically?
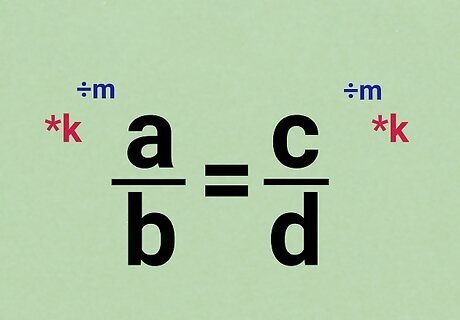
Treat the proportion as an algebraic equation. Proportions are usually introduced in a pre-algebra class. But as you move on to algebra, you'll learn that a proportion is just one kind of algebraic equation. For any algebraic equation, there's one big rule: You can change the left hand side of the equation, as long as you do the same math to the right hand side.
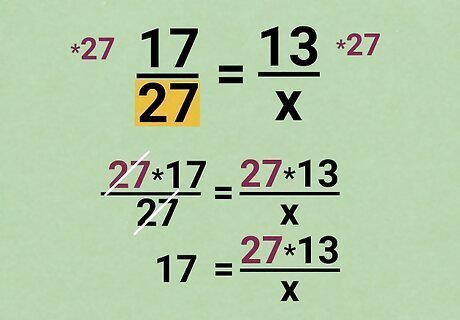
Multiply each side by a denominator. When solving for an unknown value x {\displaystyle x} x in an algebraic equation, your goal is to get x {\displaystyle x} x alone on one side. When the x {\displaystyle x} x is stuck inside a fraction, like in all proportion problems, a good way to start is to cancel out those fractions. For example, start with the proportion 17 27 = 13 x {\displaystyle {\frac {17}{27}}={\frac {13}{x}}} {\displaystyle {\frac {17}{27}}={\frac {13}{x}}}. To get rid of the fraction on the left, multiply both sides by 27: 27 × 17 27 = 27 × 13 x {\displaystyle {\frac {27\times 17}{27}}={\frac {27\times 13}{x}}} {\displaystyle {\frac {27\times 17}{27}}={\frac {27\times 13}{x}}} The 27s on the left cancel out: 17 = 27 × 13 x {\displaystyle 17={\frac {27\times 13}{x}}} {\displaystyle 17={\frac {27\times 13}{x}}}
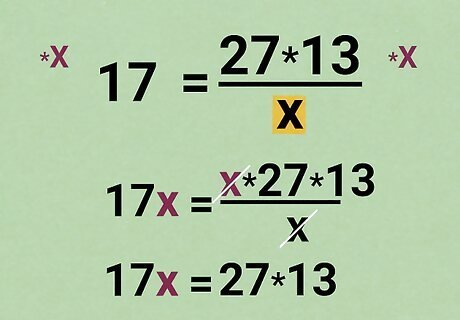
Multiply each side by the other denominator. This will get rid of the other fraction. You can do this even if the denominator is the x {\displaystyle x} x, as shown here: x × 17 = x × 27 × 13 x {\displaystyle x\times 17={\frac {x\times 27\times 13}{x}}} {\displaystyle x\times 17={\frac {x\times 27\times 13}{x}}} The two x {\displaystyle x} xs on the right cancel out: 17 x = 27 × 13 {\displaystyle 17x=27\times 13} {\displaystyle 17x=27\times 13}
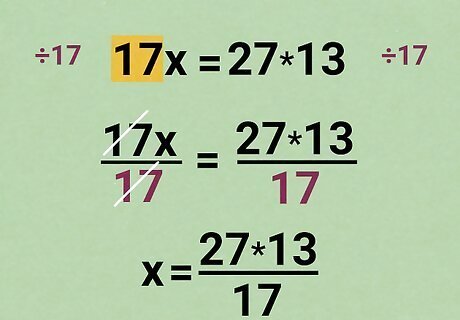
Divide to get x {\displaystyle x} x by itself. Now you should have one side of the equation that's just x {\displaystyle x} x multiplied by another number. Divide each side by that number to get x {\displaystyle x} x alone: 17 x 17 = 27 × 13 17 {\displaystyle {\frac {17x}{17}}={\frac {27\times 13}{17}}} {\displaystyle {\frac {17x}{17}}={\frac {27\times 13}{17}}} The 17s on the left cancel out: x = 27 × 13 17 {\displaystyle x={\frac {27\times 13}{17}}} {\displaystyle x={\frac {27\times 13}{17}}}
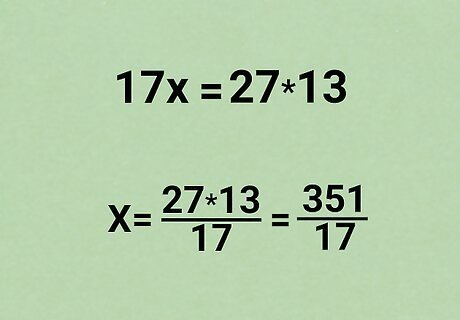
Simplify your answer or leave as-is. You can now plug your result into a calculator (or calculate by hand) and find the value of x {\displaystyle x} x. Sometimes, the answer won't simplify to a whole number or even an easy decimal. In that case, it's best to leave your answer as a fraction. x = 27 × 13 17 = 351 17 {\displaystyle x={\frac {27\times 13}{17}}={\frac {351}{17}}} {\displaystyle x={\frac {27\times 13}{17}}={\frac {351}{17}}} One big advantage to this method is that it works even when x {\displaystyle x} x is a difficult number like this. But if this didn't make much sense to you, that's okay: most teachers and textbooks start with the other methods above and teach you algebra a little later.
How do you solve a proportion with a variable on both sides?
Realize your goal is to get the variable on one side. More difficult proportion problems have an x {\displaystyle x} x on both sides of the equal sign. This works just like any proportion, but you'll have to use algebra to handle the variable x {\displaystyle x} x. Your goal is to get every x {\displaystyle x} x in the equation onto one side, so you can simplify it into one x {\displaystyle x} x and find the answer.
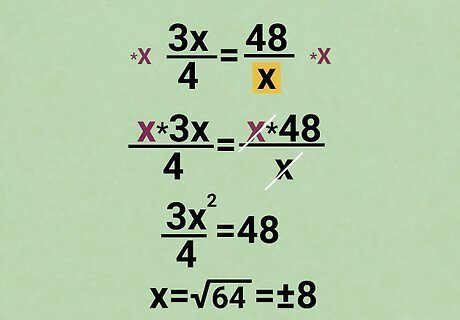
If one x {\displaystyle x} x is a denominator, multiply both sides by x {\displaystyle x} x. If the bottom of one fraction is x {\displaystyle x} x, then this will already get the x {\displaystyle x} x on one side. From that point on, normal algebra will get you to the answer: 3 x 4 = 48 x {\displaystyle {\frac {3x}{4}}={\frac {48}{x}}} {\displaystyle {\frac {3x}{4}}={\frac {48}{x}}} Multiply by x {\displaystyle x} x on both sides: x × 3 x 4 = x × 48 x {\displaystyle x\times {\frac {3x}{4}}=x\times {\frac {48}{x}}} {\displaystyle x\times {\frac {3x}{4}}=x\times {\frac {48}{x}}} Simplify: 3 x 2 4 = 48 {\displaystyle {\frac {3x^{2}}{4}}=48} {\displaystyle {\frac {3x^{2}}{4}}=48} Multiply by 4 on both sides: 4 × 3 x 2 4 = 4 × 48 {\displaystyle 4\times {\frac {3x^{2}}{4}}=4\times 48} {\displaystyle 4\times {\frac {3x^{2}}{4}}=4\times 48} Simplify: 3 x 2 = 192 {\displaystyle 3x^{2}=192} {\displaystyle 3x^{2}=192} Divide by 3 on both sides: 3 x 2 3 = 192 3 {\displaystyle {\frac {3x^{2}}{3}}={\frac {192}{3}}} {\displaystyle {\frac {3x^{2}}{3}}={\frac {192}{3}}} Simplify: x 2 = 64 {\displaystyle x^{2}=64} {\displaystyle x^{2}=64} Find the square root: x = 64 = ± 8 {\displaystyle x={\sqrt {64}}=\pm 8} {\displaystyle x={\sqrt {64}}=\pm 8}
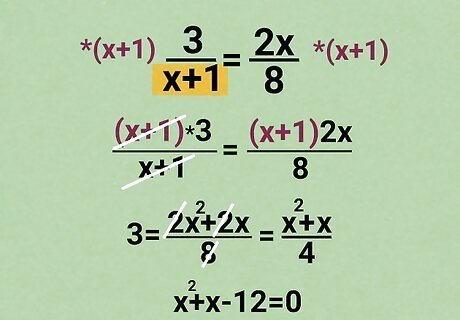
Otherwise, multiply by the entire denominator with x {\displaystyle x} x. Multiplying by only part of the denominator will not help you get rid of the fraction. Always multiply by the entire denominator: Warning: This is a difficult example. If you haven't learned about quadratic equations yet, you might want to skip this part. 3 x + 1 = 2 x 8 {\displaystyle {\frac {3}{x+1}}={\frac {2x}{8}}} {\displaystyle {\frac {3}{x+1}}={\frac {2x}{8}}} Multiply by ( x + 1 ) {\displaystyle (x+1)} (x+1): ( x + 1 ) 3 x + 1 = 2 x ( x + 1 ) 8 {\displaystyle (x+1){\frac {3}{x+1}}={\frac {2x(x+1)}{8}}} {\displaystyle (x+1){\frac {3}{x+1}}={\frac {2x(x+1)}{8}}} Simplify. Remember to multiply 2 x {\displaystyle 2x} 2x with both terms in the parentheses, and add the results together: 3 = 2 x 2 + 2 x 8 {\displaystyle 3={\frac {2x^{2}+2x}{8}}} {\displaystyle 3={\frac {2x^{2}+2x}{8}}} The fraction on the right has terms that are all divisible by 2. Simplify: 3 = x 2 + x 4 {\displaystyle 3={\frac {x^{2}+x}{4}}} {\displaystyle 3={\frac {x^{2}+x}{4}}} Multiply by 4 on both sides: 4 × 3 = 4 × x 2 + x 4 {\displaystyle 4\times 3=4\times {\frac {x^{2}+x}{4}}} {\displaystyle 4\times 3=4\times {\frac {x^{2}+x}{4}}} Simplify: 12 = x 2 + x {\displaystyle 12=x^{2}+x} {\displaystyle 12=x^{2}+x} Subtract 12 to get zero on one side: x 2 + x − 12 = 0 {\displaystyle x^{2}+x-12=0} {\displaystyle x^{2}+x-12=0} You can now solve this as a quadratic equation, using any method that you've learned. For example, you can factor this as ( x + 4 ) ( x − 3 ) = 0 {\displaystyle (x+4)(x-3)=0} {\displaystyle (x+4)(x-3)=0}, then solve for x + 4 = 0 {\displaystyle x+4=0} {\displaystyle x+4=0} and x − 3 = 0 {\displaystyle x-3=0} {\displaystyle x-3=0} to get your two answers, x = − 4 {\displaystyle x=-4} {\displaystyle x=-4} and x = 3 {\displaystyle x=3} {\displaystyle x=3}.




















Comments
0 comment