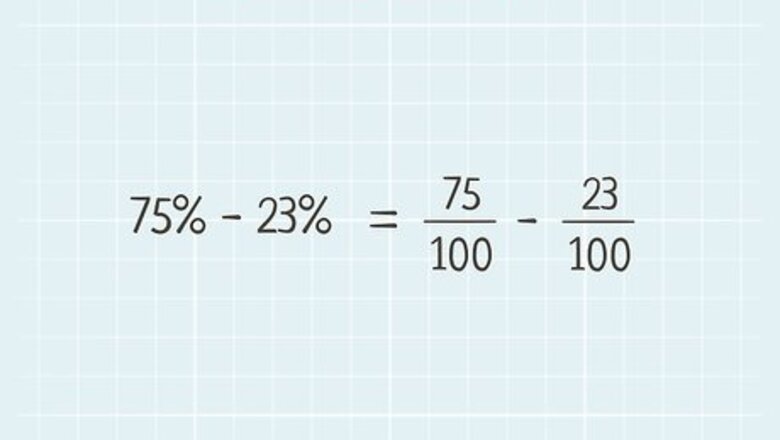
views
Converting to a Fraction

Understand a percentage as a fraction, as a number out of 100. So convert a percentage to a fraction, place the percent in the numerator, and 100 in the denominator. For example, 75 % − 23 % {\displaystyle 75\%-23\%} 75\%-23\% is the same as 75 100 − 23 100 {\displaystyle {\frac {75}{100}}-{\frac {23}{100}}} {\frac {75}{100}}-{\frac {23}{100}}.

Subtract the numerators. When subtracting fractions that have the same denominator, you simply subtract the numerators, then place the difference over the original denominator. For example, since 75 − 23 = 52 {\displaystyle 75-23=52} 75-23=52, you know that 75 100 − 23 100 = 52 100 {\displaystyle {\frac {75}{100}}-{\frac {23}{100}}={\frac {52}{100}}} {\frac {75}{100}}-{\frac {23}{100}}={\frac {52}{100}}.

Do NOT simplify. A percent is a number out of 100. To convert the fraction back to a percent, simply take the numerator and label it as a percent. For example, 52 100 {\displaystyle {\frac {52}{100}}} {\frac {52}{100}} converted to a percent is 52 % {\displaystyle 52\%} 52\%.
Converting to a Decimal

Convert the percentages to decimals. To convert a percentage to a decimal, think of the percent as a whole number, then move the decimal point two places to the left. Remember that, even though a whole number does not show a decimal point, one is understood to the right of the number in the ones place (for example 66 = 66.00). For example, 68 % − 9.5 % {\displaystyle 68\%-9.5\%} 68\%-9.5\% is the same as .68 − .095 {\displaystyle .68-.095} .68-.095 (or 68 hundredths minus 95 thousandths).

Subtract the decimals. You can use a calculator to do this quickly. You can also do it by hand. Set up the problem vertically. Align the decimal points in each number, then subtract as usual. Drop the decimal point down into your answer. For example: 0.680 − 0.095 0.585 {\displaystyle {\begin{array}{r}0.680\\-0.095\\\hline \\0.585\end{array}}} {\begin{array}{r}0.680\\-0.095\\\hline \\0.585\end{array}}

Convert back into a percentage. To do this, move the decimal place back two places to the right. Take this answer and label it as a percent. For example, to convert 0.585 {\displaystyle 0.585} 0.585 to a percent, move the decimal place two places to the right: 58.5 {\displaystyle 58.5} 58.5. So, 68 % − 9.5 % = 58.5 % {\displaystyle 68\%-9.5\%=58.5\%} 68\%-9.5\%=58.5\%

Alternatively, subtract them directly. For example: 68.0 % − 9.5 % 58.5 % {\displaystyle {\begin{array}{r}68.0\%\\-9.5\%\\\hline \\58.5\%\end{array}}} {\begin{array}{r}68.0\%\\-9.5\%\\\hline \\58.5\%\end{array}}
Calculating Negative Percentages

Anticipate a negative difference. Any time you subtract a larger percentage from a smaller percentage, the difference will be negative. These situations require additional steps when subtracting. For example, you might need to subtract 123.688% from 50%. Since 123.688 is larger than 50, your answer will be negative.

Reverse the order of the minuend and subtrahend. The minuend is the number you are subtracting from, and the subtrahend is the number you are subtracting. If you are working with decimals, align the decimal points and use zeros to extend place values as needed. For example: 50.000 % − 123.688 % {\displaystyle {\begin{aligned}50.000\%\\-123.688\%\\\hline \end{aligned}}} {\begin{aligned}50.000\%\\-123.688\%\\\hline \end{aligned}} becomes 123.688 % − 50.000 % {\displaystyle {\begin{aligned}123.688\%\\-50.000\%\\\hline \end{aligned}}} {\begin{aligned}123.688\%\\-50.000\%\\\hline \end{aligned}}

Subtract as you normally would. Borrow from larger place values when necessary. You should end up with a positive number. For example: 123.688 % − 50.000 % 73.688 % {\displaystyle {\begin{aligned}123.688\%\\-50.000\%\\\hline \\73.688\%\end{aligned}}} {\begin{aligned}123.688\%\\-50.000\%\\\hline \\73.688\%\end{aligned}}

Add a negative sign to the difference. If you visualize a number line, you should see that the difference is the absolute distance between the two numbers. However, since in the original problem you begin with a smaller number and subtract a larger number, you would move left on the number line, past zero, and thus end up with a negative number. Thus, 50 % − 123.688 % = − 73.688 % {\displaystyle 50\%-123.688\%=-73.688\%} 50\%-123.688\%=-73.688\%.

Alternatively, subtract them directly. For example: 50.000 % − 123.688 % − 73.688 % {\displaystyle {\begin{array}{r}50.000\%\\-123.688\%\\\hline \\-73.688\%\end{array}}} {\begin{array}{r}50.000\%\\-123.688\%\\\hline \\-73.688\%\end{array}}
Subtracting a Percentage from a Whole

Assess what the problem is. You are likely being asked to take a percentage discount off of a price or value. For example, you might be asked what 30% off 120 dollars is.

Convert the percentage to a decimal. To do this, remove the percentage sign and think of the percent as a whole number. Then, move the decimal point two places to the left. Sometimes the percent will have a decimal already (such as in 7.5%). If there is no decimal, remember that a whole number always has an understood decimal to the right of the ones place (such as 75 = 75.00). For example, 30 % {\displaystyle 30\%} 30\% converted to a decimal is 0.30 {\displaystyle 0.30} 0.30.

Multiply the decimal by the whole value. You can multiply be a calculator, or by hand. If multiplying by hand, set up the problem like a regular multiplication problem. Multiply the numbers as usual. Your final answer should have two places to the right of its decimal point. For more information on how to multiply decimals, read Multiply Decimals. For example, 120 × 0.30 36.00 {\displaystyle {\begin{array}{r}120\\\times 0.30\\\hline \\36.00\end{array}}} {\begin{array}{r}120\\\times 0.30\\\hline \\36.00\end{array}}

Subtract the product from the whole value. The difference is the result of subtracting the percent of a value from the whole value. For example, 120 − 36 = 84 {\displaystyle 120-36=84} 120-36=84. So, 120 − 30 % = 84 {\displaystyle 120-30\%=84} 120-30\%=84.

Alternatively, realize that a 30% discount means the price or value will represent the difference: 100 % − 30 % {\displaystyle 100\%-30\%} 100\%-30\% = 70 % {\displaystyle 70\%} 70\% The price will be 70% of the original price, so simply find 70% of $120 -- using the decimal equivalent 70% = 0.70 multiply the original price -- to get the discounted price. For example, $ 120 × 0.70 $ 84.00 {\displaystyle {\begin{array}{r}\$120\\\times 0.70\\\hline \\\$84.00\end{array}}} {\begin{array}{r}\$120\\\times 0.70\\\hline \\\$84.00\end{array}}


















Comments
0 comment