How to Calculate Wavelength

Calculating Wavelength Given Speed and Frequency

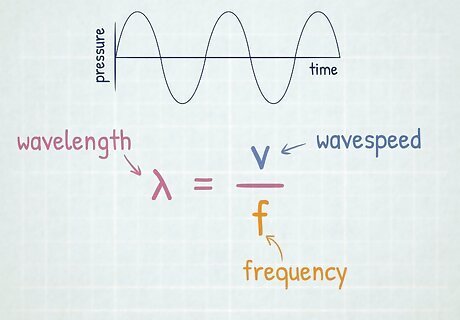
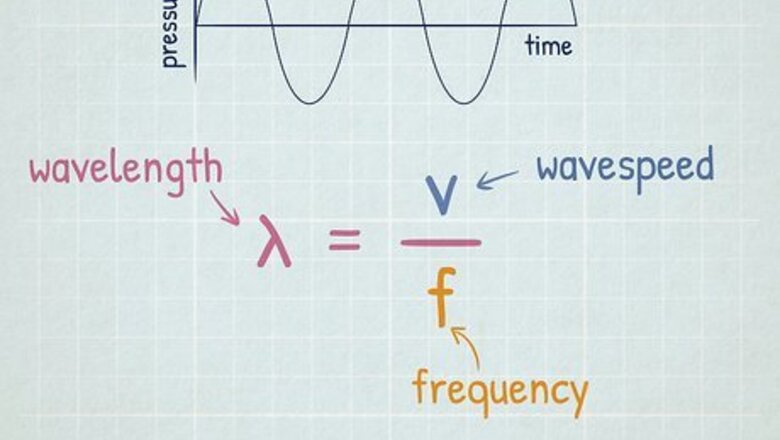
Calculate wavelength with the wavelength equation. To find the wavelength of a wave, you just have to divide the wave's speed by its frequency. The formula for calculating wavelength is: W a v e l e n g t h = W a v e s p e e d F r e q u e n c y {\displaystyle Wavelength={\frac {Wavespeed}{Frequency}}} Wavelength={\frac {Wavespeed}{Frequency}}. Wavelength is commonly represented by the Greek letter lambda, λ {\displaystyle \lambda } \lambda . Speed is commonly represented by the letter v {\displaystyle v} v. Frequency is commonly represented by the letter f {\displaystyle f} f. λ = v f {\displaystyle \lambda ={\frac {v}{f}}} \lambda ={\frac {v}{f}}

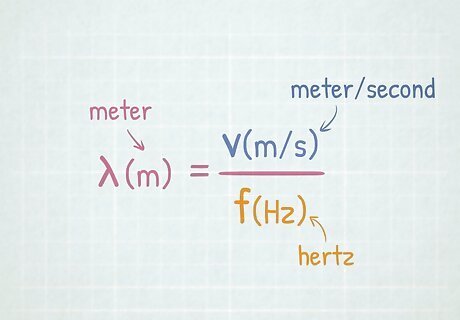
Use the correct units. Speed can be represented using both metric and imperial units. You may see it as miles per hour (mph), kilometers per hour (kph), meters per second (m/s), etc. Wavelength is almost always given in metric units: nanometers, meters, millimeters, etc. Frequency is generally expressed in Hertz (Hz) which means “per second”. Always keep units consistent across the equation. Most calculations are done using strictly metric units. If the frequency is in kilohertz (kHz) or the wave speed is in km/s you will need to convert these numbers to Hertz and m/s by multiplying by 1000 (10 kHz = 10,000 Hz).

Plug the known quantities into the equation and solve. If you want to calculate the wavelength of a wave, then all you have to do is plug the wave's speed and wave's frequency into the equation. Dividing speed by frequency gives you the wavelength. For example: Find the wavelength of a wave traveling at 20 m/s at a frequency of 5 Hz. W a v e l e n g t h = W a v e s p e e d F r e q u e n c y {\displaystyle Wavelength={\frac {Wavespeed}{Frequency}}} Wavelength={\frac {Wavespeed}{Frequency}} λ = v f {\displaystyle \lambda ={\frac {v}{f}}} \lambda ={\frac {v}{f}} λ = 20 m / s 5 H z {\displaystyle \lambda ={\frac {20m/s}{5Hz}}} \lambda ={\frac {20m/s}{5Hz}} λ = 4 m {\displaystyle \lambda =4m} \lambda =4m

Use this equation to solve for speed or frequency. You can rearrange this equation and solve for speed or frequency if given wavelength. To calculate speed given frequency and wavelength, use v = λ ∗ f {\displaystyle v={\lambda }*{f}} v={\lambda }*{f}. To calculate frequency given speed and wavelength, use f = v λ {\displaystyle f={\frac {v}{\lambda }}} f={\frac {v}{\lambda }}. For example: Find the speed of a wave with wavelength 450 nm and frequency 45 Hz. v = λ ∗ f = 450 n m ∗ 45 H z = 20 , 250 n m / s <= 20.25 u m / s {\displaystyle v={\lambda }*{f}={450nm}*{45Hz}=20,250nm/s<=20.25um/s} v={\lambda }*{f}={450nm}*{45Hz}=20,250nm/s. For example: Find the frequency of a wave with wavelength 2.5 m and speed 50 m/s. f = v λ = 50 m / s 2.5 m = 20 H z {\displaystyle f={\frac {v}{\lambda }}={\frac {50m/s}{2.5m}}=20Hz} f={\frac {v}{\lambda }}={\frac {50m/s}{2.5m}}=20Hz.

Calculating Wavelength Given Energy of a Photon

Calculate wavelength with the energy equation. The formula for energy involving wavelength is E = h c λ {\displaystyle E={\frac {hc}{\lambda }}} E={\frac {hc}{\lambda }} where E {\displaystyle E} E is the energy of the system in Joules (J), h {\displaystyle h} h is Planck’s constant: 6.626 x 10 Joule seconds (J s), c {\displaystyle c} c is the speed of light in a vacuum: 3.0 x 10 meters per second (m/s), and λ {\displaystyle \lambda } \lambda is the wavelength in meters (m). The energy of a photon is usually given to solve these types of problems.

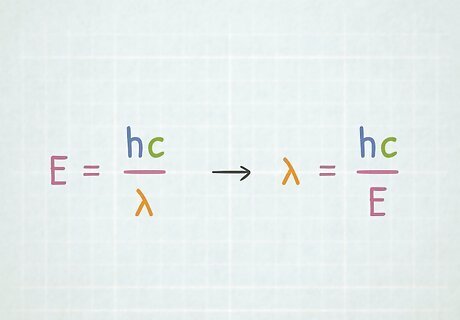
Rearrange to solve for wavelength. You can rearrange the equation with algebra to solve for wavelength. If you multiply both sides of the equation by wavelength and then divide both sides by energy, you are left with λ = h c E {\displaystyle \lambda ={\frac {hc}{E}}} \lambda ={\frac {hc}{E}}. If you know the energy of the photon, you can calculate its wavelength. This equation can also be used to determine the maximum wavelength of light necessary to ionize metals. Simply use the energy required for ionization and solve for the corresponding wavelength.

Plug in the known variables and solve. Once you have rearranged the equation, you can solve for the wavelength by plugging in the variables for energy. Because the other two variables are constants, they are always the same. To solve, multiply the constants together and then divide by the energy. For example: Find the wavelength of a photon with an energy of 2.88 x 10 J. λ = h c E {\displaystyle \lambda ={\frac {hc}{E}}} \lambda ={\frac {hc}{E}}= ( 6.626 ∗ 10 − 34 ) ( 3.0 ∗ 10 8 ) ( 2.88 ∗ 10 − 19 ) {\displaystyle {\frac {(6.626*10^{-34})(3.0*10^{8})}{(2.88*10^{-19})}}} {\frac {(6.626*10^{{-34}})(3.0*10^{{8}})}{(2.88*10^{{-19}})}} = ( 19.878 ∗ 10 − 26 ) ( 2.88 ∗ 10 − 19 ) {\displaystyle ={\frac {(19.878*10^{-26})}{(2.88*10^{-19})}}} ={\frac {(19.878*10^{{-26}})}{(2.88*10^{{-19}})}} = 6.90 ∗ 10 − 7 m e t e r s {\displaystyle =6.90*10^{-7}meters} =6.90*10^{{-7}}meters. Convert to nanometers by multiplying by 10. The wavelength equals 690 nm.

Catching Mistakes

Check your answer by multiplying the wavelength by the frequency. If you found the right value for the wavelength, multiplying by the frequency should get you the wave speed you started with. If it doesn't, check your math. If you are using a calculator, make sure you have typed the numbers in correctly. For example: What is the wavelength of a 70 Hertz sound wave traveling at 343 meters per second? You follow the instructions above and get an answer of 4.9 meters. Check your work by calculating 4.9 meters x 70 Hz = 343 meters/second. This is the wave speed you started with, so your answer is correct.

Use scientific notation to avoid calculator rounding errors. Wavelength calculations often involve very large numbers, especially if you're working with light speed. This can lead to rounding errors on your calculator. Prevent this by writing your numbers in scientific notation and double checking the significant digits. For example: Light travels through water at about 225,000,000 meters per second. If the wave's frequency is 4 x 10 Hz, what is its wavelength? The wave speed in scientific notation = 2.25 x 10. The frequency is already written in scientific notation. W a v e l e n g t h = w a v e s p e e d f r e q u e n c y {\displaystyle Wavelength={\frac {wavespeed}{frequency}}} Wavelength={\frac {wavespeed}{frequency}} = 2.25 ∗ 10 8 4 ∗ 10 14 = 2.25 4 ∗ 10 6 {\displaystyle ={\frac {2.25*10^{8}}{4*10^{14}}}={\frac {2.25}{4*10^{6}}}} ={\frac {2.25*10^{8}}{4*10^{{14}}}}={\frac {2.25}{4*10^{6}}} = 0.563 ∗ 10 − 6 m e t e r s {\displaystyle =0.563*10^{-6}meters} =0.563*10^{{-6}}meters = 5.63 ∗ 10 − 7 m e t e r s {\displaystyle =5.63*10^{-7}meters} =5.63*10^{{-7}}meters.

Do not change frequency when a wave enters a different medium. Many word problems involve a wave that crosses the boundary from one medium to another. A common mistake here is calculating a new frequency for the wave. In fact, the frequency of the wave remains the same when it crosses the boundary, while the wavelength and wave speed change. For example: A light wave with frequency f, speed v, and wavelength λ crosses from air to a medium with refractive index 1.5. How do these three values change? The new speed is equal to v 1.5 {\displaystyle {\frac {v}{1.5}}} {\frac {v}{1.5}}. The frequency remains constant at f. The new wavelength is equal to n e w s p e e d n e w f r e q u e n c y = v 1.5 f = v 1.5 f {\displaystyle {\frac {newspeed}{newfrequency}}={\frac {\frac {v}{1.5}}{f}}={\frac {v}{1.5f}}} {\frac {newspeed}{newfrequency}}={\frac {{\frac {v}{1.5}}}{f}}={\frac {v}{1.5f}}.

Check your units. The units you use will often tell you what to do when you are solving a problem. If they do not make sense when you finish, then check to see if you used the right units. For example, perhaps you used Joules when you should have used Hertz, so you ended up with the incorrect answer.