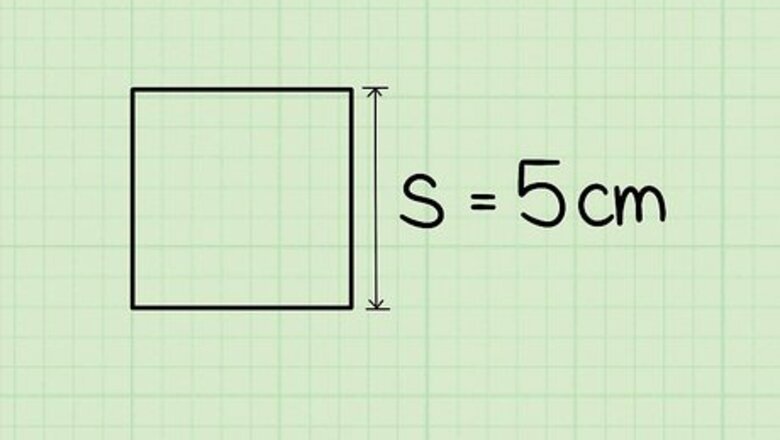
views
d
=
s
2
{\displaystyle d=s{\sqrt {2}}}
, where
s
{\displaystyle s}
equals one side length of the square. Sometimes, however, you might be asked to find the length of the diagonal given another value, such as the perimeter or area of the square. In these instances it is necessary to use different formulas first, so that you can determine the side length before using the diagonal formula.
If You Know the Length of One Side
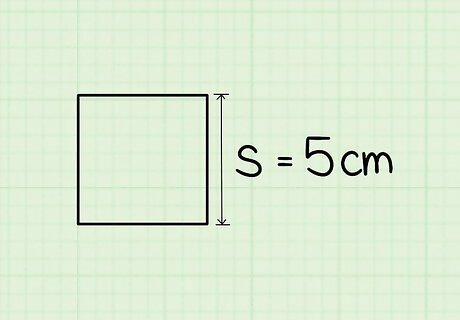
Find the length of one side of the square. This will probably be given to you. If you are working with a square in the real world, use a ruler or piece of measuring tape to find the length. Since all four sides of the square are the same length, you can use any side of the square. If you do not know the length of one side of the square, you cannot use this method. For example, you might want to find the length of the diagonal of a square that has sides 5 centimeters long.
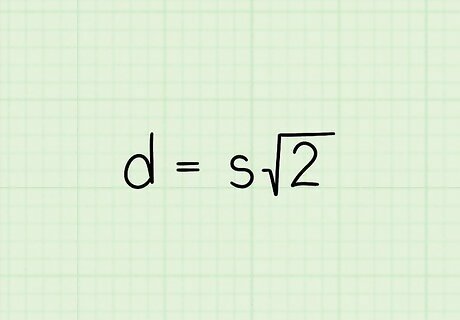
Set up the formula d = s 2 {\displaystyle d=s{\sqrt {2}}} d=s{\sqrt {2}}. In the formula d {\displaystyle d} d equals the length of the diagonal and s {\displaystyle s} s equals one side of the square. This formula is derived from the Pythagorean Theorem ( a 2 + b 2 = c 2 ) {\displaystyle a^{2}+b^{2}=c^{2})} a^{2}+b^{2}=c^{2}). A diagonal divides a square into two congruent right triangles, thus, you can use the side lengths of the square to find the length of the diagonal (which would be the hypotenuse of the right triangle).
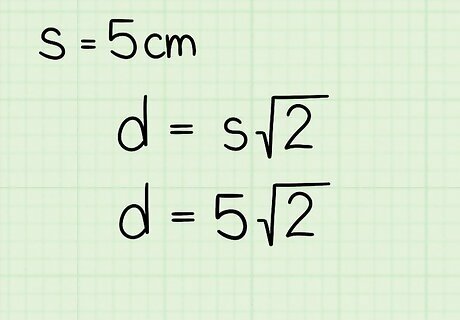
Plug the side length of the square into the formula. Make sure you are substituting for the variable s {\displaystyle s} s. For example, if the square has a side length of 5 centimeters, set up the formula like this: d = 5 2 {\displaystyle d=5{\sqrt {2}}} d=5{\sqrt {2}}
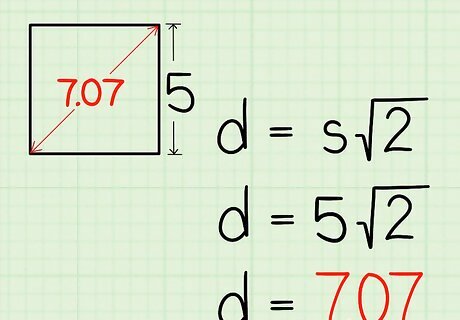
Multiply the length of the side by 2 {\displaystyle {\sqrt {2}}} {\sqrt {2}}. This will give you the length of the diagonal. It’s best to perform the calculation on a calculator, so that you can get a more precise result. If you don’t have a calculator, you can round 2 {\displaystyle {\sqrt {2}}} {\sqrt {2}} to 1.414. For example, if you are calculating the diagonal of a 5-centimeter square, your formula will look like this: d = 5 2 {\displaystyle d=5{\sqrt {2}}} d=5{\sqrt {2}} d = 7.07 {\displaystyle d=7.07} d=7.07So, the diagonal of the square is 7.07 centimeters long.
If You Know the Perimeter
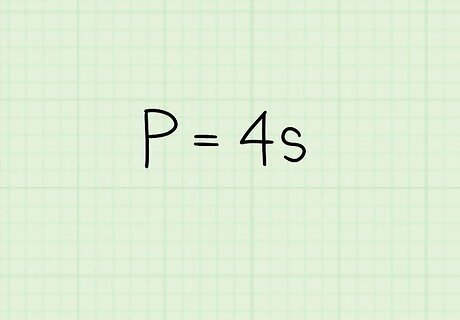
Set up the formula for the perimeter of a square. The formula is P = 4 s {\displaystyle P=4s} P=4s, where P {\displaystyle P} P equals the perimeter of the square, and s {\displaystyle s} s equals the length of one side of the square. This method only works if you are given the perimeter of the square. To find the length of the diagonal, you must first find the length of one side of the square, so you need to set up the perimeter formula and solve for s {\displaystyle s} s.
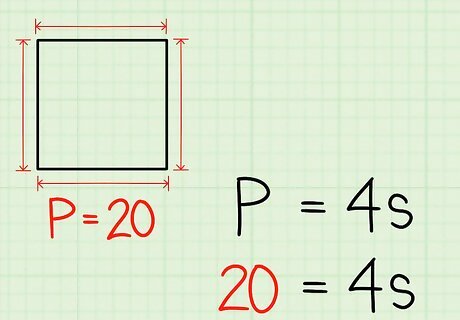
Plug the length of the perimeter into the formula. Make sure you are substituting for the variable P {\displaystyle P} P. For example, if the perimeter of the square is 20 centimeters, your formula will look like this: 20 = 4 s {\displaystyle 20=4s} 20=4s
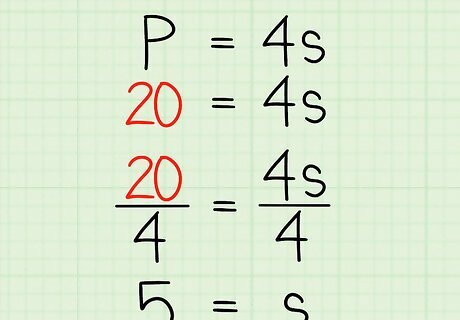
Solve for s {\displaystyle s} s. To do this, divide each side of the equation by 4. This will give you the length of one side of the square. For example: 20 = 4 s {\displaystyle 20=4s} 20=4s 20 4 = 4 s 4 {\displaystyle {\frac {20}{4}}={\frac {4s}{4}}} {\frac {20}{4}}={\frac {4s}{4}} 5 = s {\displaystyle 5=s} 5=s
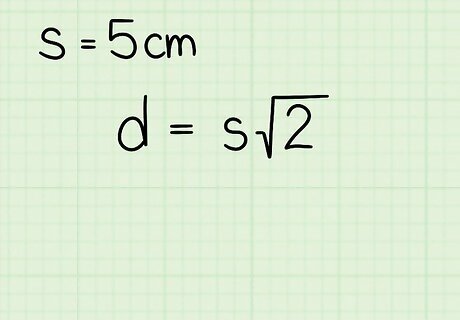
Set up the formula d = s 2 {\displaystyle d=s{\sqrt {2}}} d=s{\sqrt {2}}. In the formula d {\displaystyle d} d equals the length of the diagonal and s {\displaystyle s} s equals one side of the square. This formula is derived from the Pythagorean Theorem ( a 2 + b 2 = c 2 ) {\displaystyle a^{2}+b^{2}=c^{2})} a^{2}+b^{2}=c^{2}). A diagonal divides a square into two congruent right triangles, thus, you can use the side lengths of the square to find the length of the diagonal (which would be the hypotenuse of the right triangle). EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Use this visual trick to understand the Pythagorean Theorem. Imagine a right triangle with squares constructed on each leg and the hypotenuse. by rearranging the smaller squares within the larger square, the areas of the smaller squares (a² and b²) will add up visually to the area of the larger square (c²).
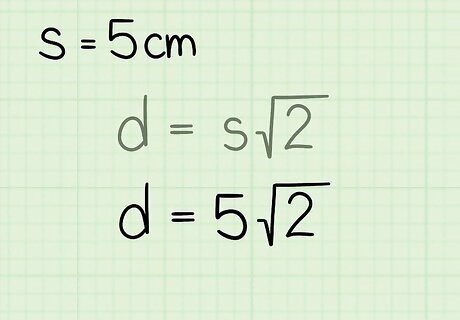
Plug the side length of the square into the formula. Make sure you are substituting for the variable s {\displaystyle s} s. For example, if the square has a side length of 5 centimeters, set up the formula like this: d = 5 2 {\displaystyle d=5{\sqrt {2}}} d=5{\sqrt {2}}
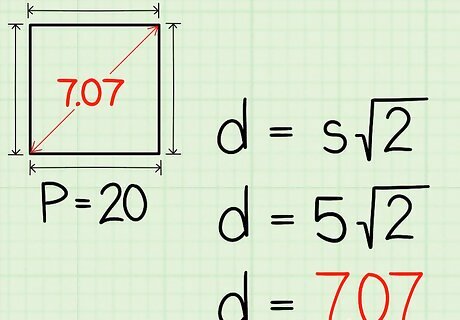
Multiply the length of the side by 2 {\displaystyle {\sqrt {2}}} {\sqrt {2}}. This will give you the length of the diagonal. It’s best to perform the calculation on a calculator, so that you can get a more precise result. If you don’t have a calculator, you can round 2 {\displaystyle {\sqrt {2}}} {\sqrt {2}} to 1.414. For example, if you are calculating the diagonal of a 5-centimeter square, your formula will look like this: d = 5 2 {\displaystyle d=5{\sqrt {2}}} d=5{\sqrt {2}} d = 7.07 {\displaystyle d=7.07} d=7.07So, the diagonal of the square is 7.07 centimeters long.
If You Know the Area
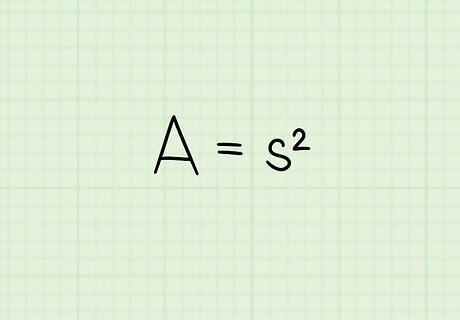
Set up the formula for the area of a square. The formula is A = s 2 {\displaystyle A=s^{2}} A=s^{{2}}, where A {\displaystyle A} A equals the area of the square, and s {\displaystyle s} s equals the length of one side of the square. This method only works if you are given the area of the square. To find the length of the diagonal, you have to first find the length of one side of the square, which is why you must set up the area formula and solve for s {\displaystyle s} s.
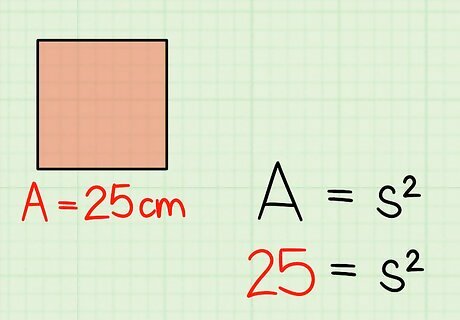
Plug the area measurement into the formula. Make sure you are substituting for the variable A {\displaystyle A} A. For example, if the area of the square is 25 square centimeters, your formula will look like this: 25 = s 2 {\displaystyle 25=s^{2}} 25=s^{{2}}
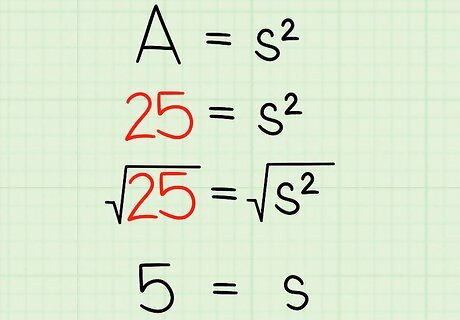
Solve for s {\displaystyle s} s. To do this, find the square root of the area. This will give you the length of one side of the square. To find the square root, use a calculator. If you need help calculating the square root by hand, read Calculate a Square Root by Hand. For example: 25 = s 2 {\displaystyle 25=s^{2}} 25=s^{{2}} 25 = s 2 {\displaystyle {\sqrt {25}}={\sqrt {s^{2}}}} {\sqrt {25}}={\sqrt {s^{{2}}}} 5 = s {\displaystyle 5=s} 5=s
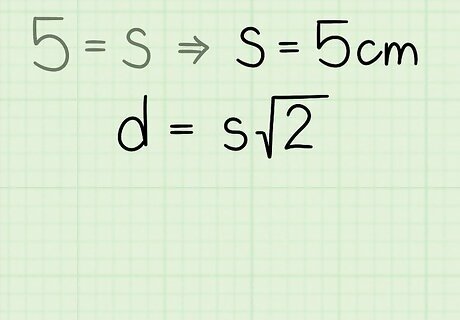
Set up the formula d = s 2 {\displaystyle d=s{\sqrt {2}}} d=s{\sqrt {2}}. In the formula d {\displaystyle d} d equals the length of the diagonal and s {\displaystyle s} s equals one side of the square. This formula is derived from the Pythagorean Theorem ( a 2 + b 2 = c 2 ) {\displaystyle a^{2}+b^{2}=c^{2})} a^{2}+b^{2}=c^{2}). A diagonal divides a square into two congruent right triangles, thus, you can use the side lengths of the square to find the length of the diagonal (which would be the hypotenuse of the right triangle).
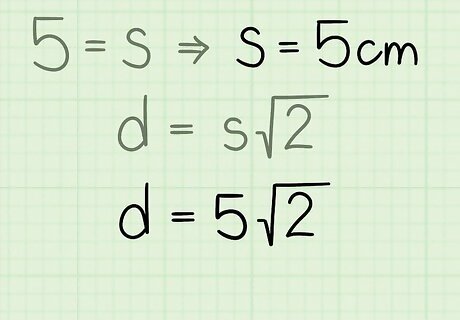
Plug the side length of the square into the formula. Make sure you are substituting for the variable s {\displaystyle s} s. For example, if the square has a side length of 5 centimeters, set up the formula like this: d = 5 2 {\displaystyle d=5{\sqrt {2}}} d=5{\sqrt {2}}
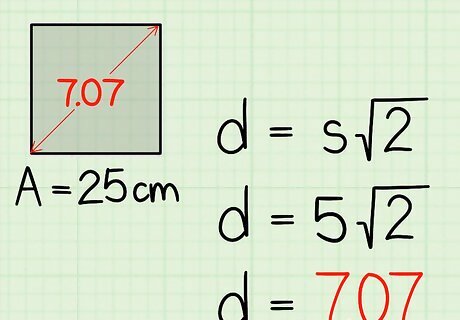
Multiply the length of the side by 2 {\displaystyle {\sqrt {2}}} {\sqrt {2}}. This will give you the length of the diagonal. *It’s best to perform the calculation on a calculator, so that you can get a more precise result. If you don’t have a calculator, you can round 2 {\displaystyle {\sqrt {2}}} {\sqrt {2}} to 1.414. For example, if you are calculating the diagonal of a 5-centimeter square, your formula will look like this: d = 5 2 {\displaystyle d=5{\sqrt {2}}} d=5{\sqrt {2}} d = 7.07 {\displaystyle d=7.07} d=7.07So, the diagonal of the square is 7.07 centimeters long.

















Comments
0 comment